正态分布是属于连续分布的一种。与连续分布相对的是离散分布。

连续分布的数据是通过测量可得的数据，测量结果取决于测量精度的要求，它是连绵不断的分布。而离散分布的数据是通过计数得到的，数据之间有明确的间隔。

举个例子，一个画室之中只有A君和B君在。那么A君和B君这是两个人。两个人的数据就是离散的，因为不可能有1.5个A君或者0.75个B君在。1个人和另外一个人，就是1和2之间有着明确的间距。但是A君站在B君的不远处，距离会是3.15米，但是再精确一点，是3.1564米，再继续精确，是3.1564287米，一直下去可以会是3.15642874624……米，这个数据就是连续的。

正态分布是连续分布的理想模型。它又称为高斯分布。其分布呈钟形曲线，通过参数均值μ（读作缪）来确定曲线的中央位置，通过标准差σ（读作西格玛，没错，就是那个六西格玛的西格玛）来指出分散性。

分布图形如下，标准正态分布就是指均值为0 ，标准差为1的分布。以0为中心，向两边对称分布。

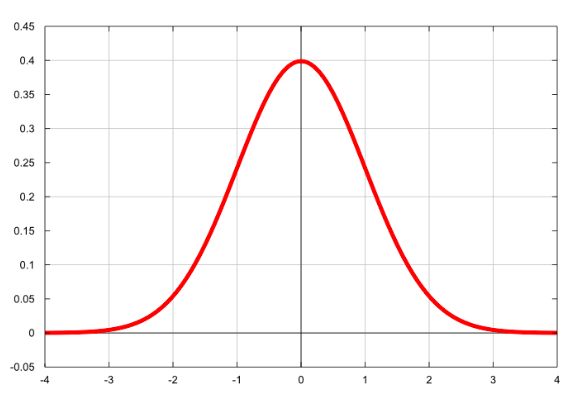
图3-17 标准正态分布图

在在某些论调中，有种误导：就是一般来说，非正态分布情况下，数据样本足够大的话（样本大于30），那么其分布就会近似正态。因此，总有人以为抽取30个样本数值就可以用来计算安全库存公式。

事实上，所谓30个样本这种说法是根据中心极限定理而来的。中心极限定理提出了在一定的条件下，大量独立随机变量的平均数是以正态分布为极限。大意可以这么理解：如果样本的数量大小n≥30，且属于任何均值为μ，标准差为σ的抽样总体，这个样本均值会近似服从正态分布。

注意，是样本均值近似正态，并非样本个体。也就是如果我们有过去数年的历史数据，假设是5年（按月来说，有60个月的数据），每次抽取30个月计算其平均值，抽n次来计算，这里可以有30的n次方抽法（可重复数据），其均值组合就近似正态，而不是60个月只要有30个月的数据，这30个月就近似正态。