间歇性需求就是需求并非连续的，就是某一个时间段有这种需求，而某一个时间段却没有，需求为零。所见的场景例如汽车配件，某型号的维修备件，可能在某个时间段要维修车辆的某部分很多，因此该备用零件有需求，而在某一段时间而没有发生任何故障，不需要维修这个零件，因此这个零件的需求则为零。这种零需求甚至可能持续数段时期。

处理这种问题，最简单的就是克罗斯顿平均法。就是剔除了所有零需求之后，对此进行平均并作为下一期的预测。实际上就是一种简单的平均法。

图4-53 简单平均法和克罗斯顿平均法比较

当然，在此基础上可以根据情况进行剔除零需求后，对克罗斯顿平均法采用更进一步的平均计算，诸如移动平均，加权平均等。

除此之外，还有针对这种间隙性需求，拆分三个步骤来进行预测。首先，对需求的平均规模进行单独的指数平滑估计。其次，计算需求之间的平均间隔。然后以常数模型的形式使用它来预测未来的需求。其公式是：

是t期的估算的非零需求量，就是t-1期的估算的非零需求量。

是t期的实际值。

是t期的估算的非零需求的时间间隔，则是t-1期估算的非零需求的时间间隔。

是平滑指数，取值均在0和1之间。前者是涉及需求规模，后者则是涉及需求间隔。

则是自从上次实际非零需求以来的t期的期间数。比如有5期需求是3，0，0，0，1，那么第1期的需求3到第5期的才有了非0需求的需求1，第5期的Q值则是5-1=4

就是t期的预测值

某部件的需求情况如下，不时地产生需求，但又不时的连续时期不产生任何需求。

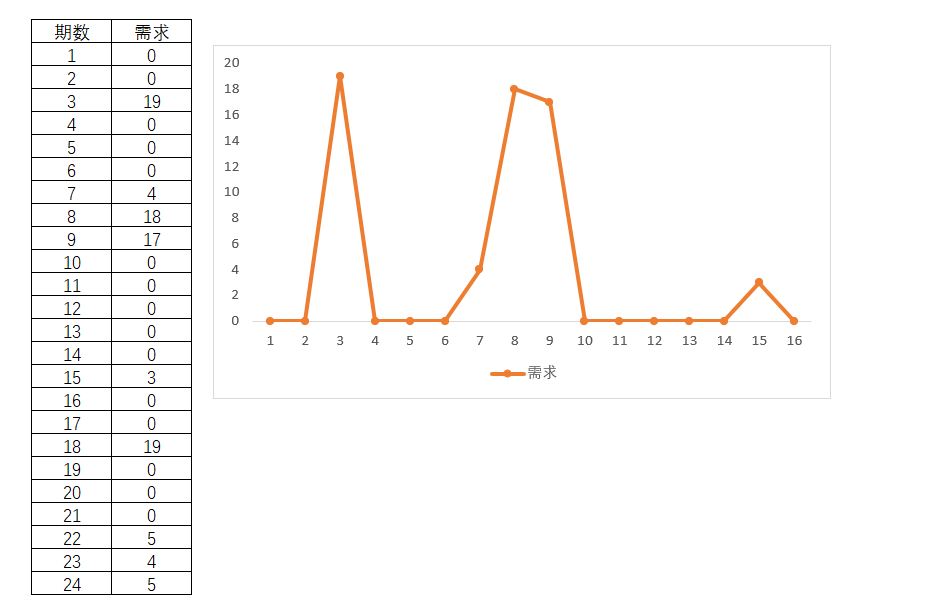
图4-54 某部件需求情况

克罗斯顿预测法的第一步，要得出Q，也就是清楚每一个非零实际需求之间的间隔期数是多少。第1期初始Q为1，那么第2期实际需求还是0，所以延续计算为2，到了第3期实际需求是19，因此零需求的计算便中止，开始重新计算为1了。

第二步，取对应的平滑指数。平滑指数的优化，可以根据得到的结果进行规划求解来寻找适合的数值。这里α取值为0.7，β取值为0.5。

第三步，就是代入相关的公式，从而计算和值。

如此类推，得到各期相应的值。

表4-52 Excel中的求解

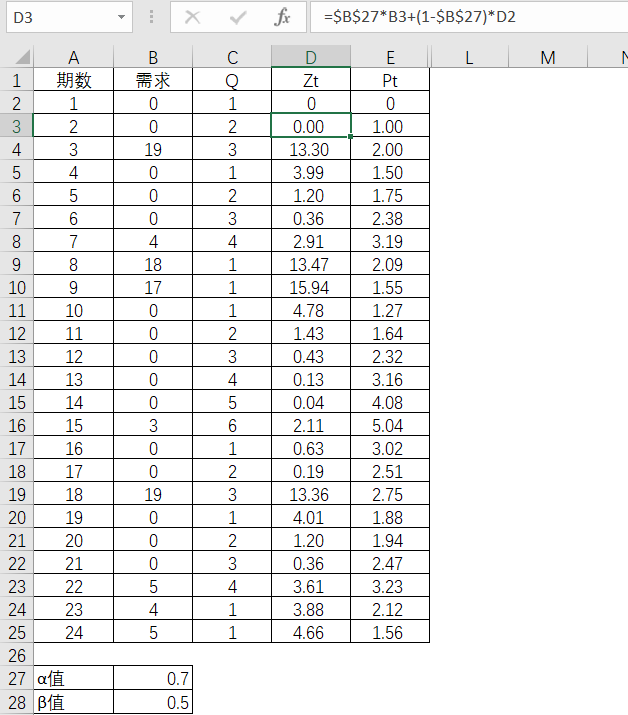
表4-53 Excel中的求解

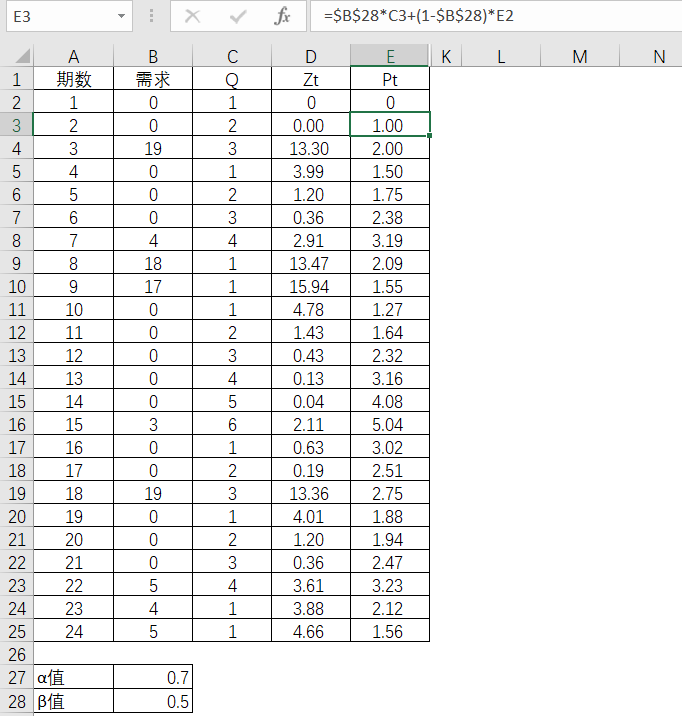
下一步就是通过t期的Z值和P值，来计算该期的预测值。如第3期的预测值则为第3期Z值除以同期的P值。

表4-54 Excel中预测值的求解

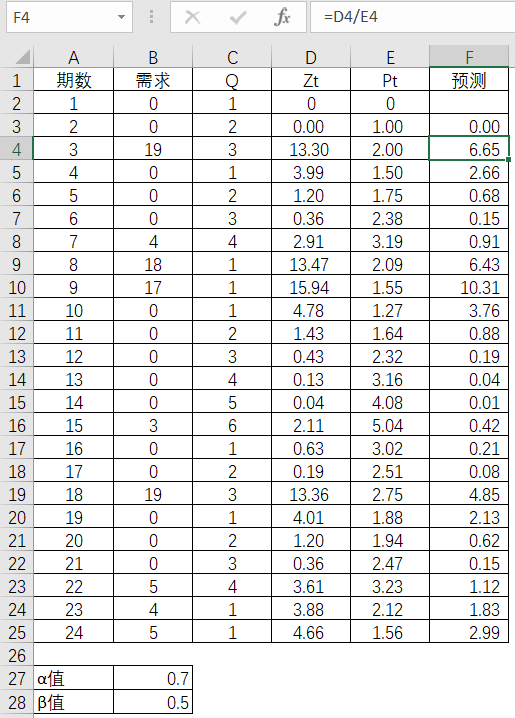
当然，由于α值和β值都是初始选择，最后通过数据规划分析，使MSE最小化，从而寻找适合的α和β值，分别为1和0.18（β值按保留两位小数）。

表4-55 MSE最优化

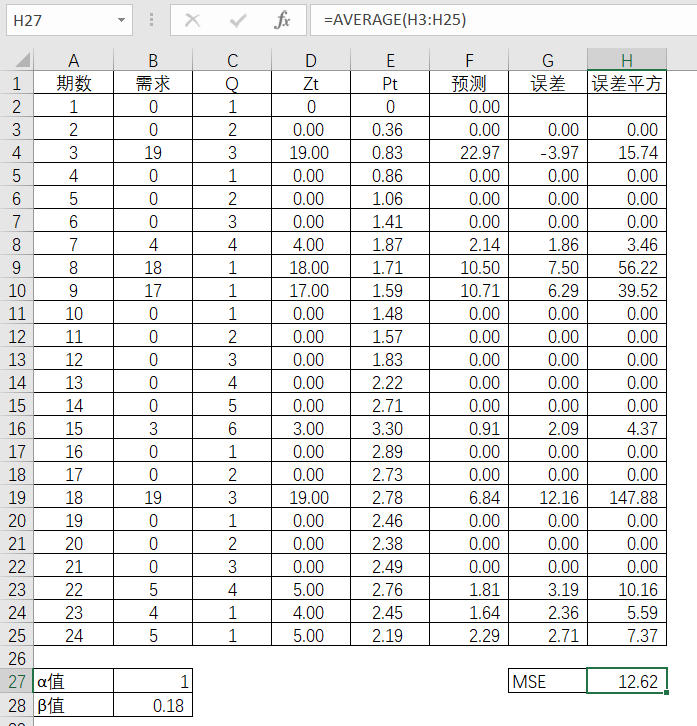
这种情况，拟合度会变得更好。其中第24期的预测值是5除以2.19，得2.29。意味着用克罗斯顿的方法，其需求预测是5个单位，时间间隔是2.19。

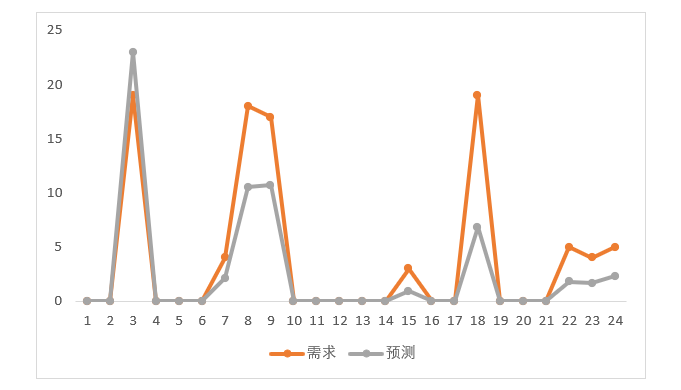
图4-55 需求和克罗斯顿预测法的比较

有了24期的数值，就可以通过指数平滑法对25期进行预测。假如第24期的实际值为0的时候，直接把第24期的预测值作为第25期的预测值。假如第24期的实际值大于0，则采用一数值平滑公式来计算第25期的预测值。其中平滑指数继续采用之前优化后所得的α值。

α值=1远比α值=0.2时波动激烈，因此继续以此进行一指数平滑。值得注意的是，克罗斯顿方法的β参数，是涉及时间间隔的参数，并非双指数平滑中代表趋势的β参数，因此不可套用。克罗斯顿方法实际上，也是一种指数平滑的方法，只是平滑的对象不同而已。

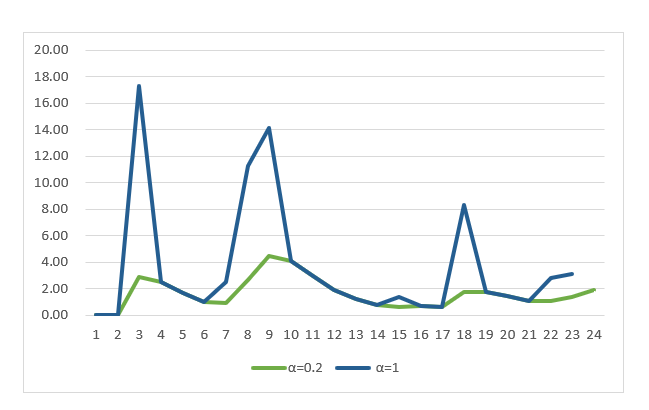
图4-56 不同α值的比较

这个克罗斯顿方法虽然在分解需求量和需求的间隔进行单独估计是被认为正确的，可是有些学者认为如果把两者作为比率来计算预测会有偏差，因此有学者（Syntetos和Boylan）提出一种新的平均估算法以克服这个问题，其预测公式演化为

因此这个公式也被称为 SBA （ Syntetos-Boylan Approximation）预测方法。这个方法消除了对非间歇性需求的偏见，尽管增加预测方差。

隙性需求的货物多属于XYZ分类中的Z分类，库存和订货策略常用的是双堆法。克罗斯顿方法是针对间隙性需求的方法，对双堆法中每堆数量的设立有着积极的指导作用。克罗斯顿法必须根据每次发生的实际情况加入，进行滚动预测，否则响应就会显得滞后。