跑步时间与摄氧量如表1-11所示。

表1-11 跑步时间与摄氧量

1.选定分析对象

分析对象的选定，可以是质量特性值与因素之间的关系、质量特性值与质量特性值之间的关系、因素与因素之间的关系。

2.收集数据，填入数据表

数据一般要在30组以上，且数据必须是对应的，并记录收集数据的日期、取样方法、测定方法等有关事项。

3.利用Mintab软件制作散布图

（1）选择“图形—散点图”，如图1-10所示。

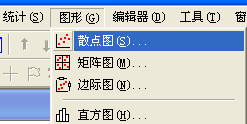
图1-10 散点图操作1

（2）选择“简单”，点击“确定”。如果选择包含回归，则得到含有一条回归线图,如图1-11所示。

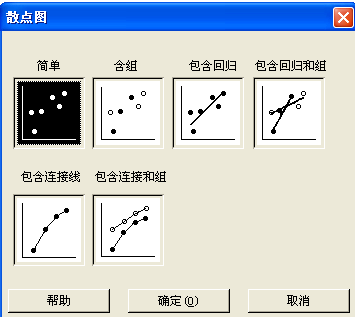
图1-11 散点图操作图2

（3）“Y变量”选择“摄氧量”；“X变量”选择“跑步时间”；点击“确定”。如图1-12、图1-13、图1-14所示。

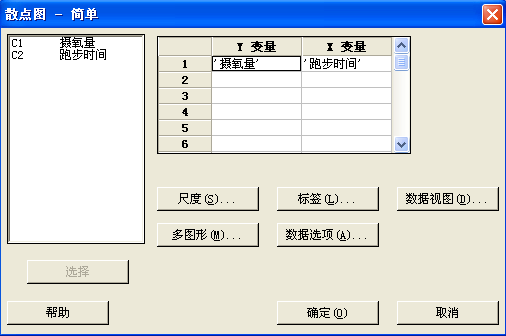
图1-12 散点图操作图3

图1-13 简单散点图4

图1-14 含回归线散点图5

（四）散布图的解析

为了准确地描述x，y相关和密切程度，我们引入一个统计量来量化它，这就是样本相关系数r。相关系数r的具体数学推导公式在此不做描述，对于实际工作中的应用，关键是要理解相关系数的含义。

相关系数r在不同取值范围时与散点图的关系大致如图1-15、图1-16、图1-17所示。

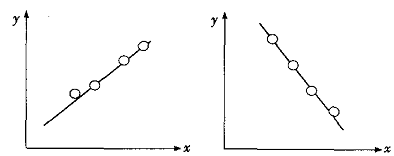
图1-15 r±1时，x,y完全线性相关散布图

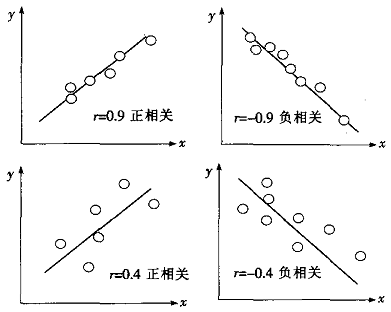
图1-16｜r|<1时，x,y线性相关散布图

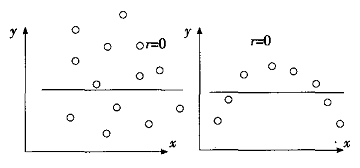
图1-17 r=0时，x,y线性相关散布图

从相关系数的定义及从上述三张图可以看出，r的绝对值越接近于1，则数据点与直线越靠拢；r的绝对值越小，则数据点与直线越远离。直到最后，如果x与y完全无关，则r应该接近于0。反之，如果r接近于0，我们不能断言“x与y完全无关”。实际上，x与y的关系很可能如图（图1-17）右图那样，是有二次函数关系的。因此正确的说法是：如果r接近于0，我们可以断言x与y非线性相关。总之，相关系数r是两个变量间线性相关关系密切程度的度量。

在实际工程中，如果知道某两个变量间没有线性相关关系，那么它们总体的相关系数应该为0。但由于实验或测量的误差，我们根据样本数据计算出来的相关系数却不会准确等于0。我们会想到：到底样本相关系数r为多大时，才可以认为x,y是在统计意义上具有线性相关关系呢？

有些书及教材中说：“只要相关系数绝对值大于0.8，二者肯定相关。”这显然是错误的。原因就在于样本相关系数r的分布与样本量密切相关，我们需要通过假设检验的方式加以判断，这里关于假设检验方式不做详细解释。

注意：x与y显着相关并不意味着x与y间一定存在因果关系，可能它们都以另一个变量为原因。例如：对于一个城市，“当日雨伞的销售量”与“当日道路上交通事故量”高度相关，但二者谁也不是另一者的原因，实际上二者都以“当日降雨情况”为原因。因此，在实际工作中，寻找原因时不能只看相关系数，还要分析变量间关系的结构。反过来说，寻找y的原因时，只可能在与y有显着密切相关关系的变量组中寻找；与y关系不密切者更不可能是y的原因。研究相关系数对于质量管理而言还是很重要的。

相关系数的计算可以通过Minitab软件来实现。选择“统计－基本统计量－相关”，选择相关变量，得到的结果如图1-18所示。

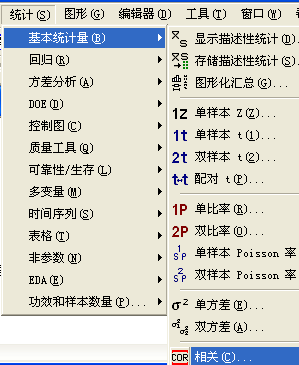
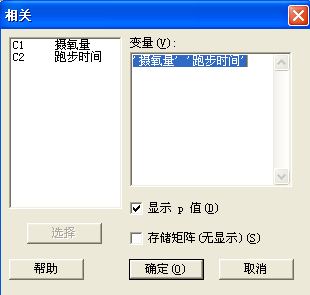
图1-18 相关性操作图

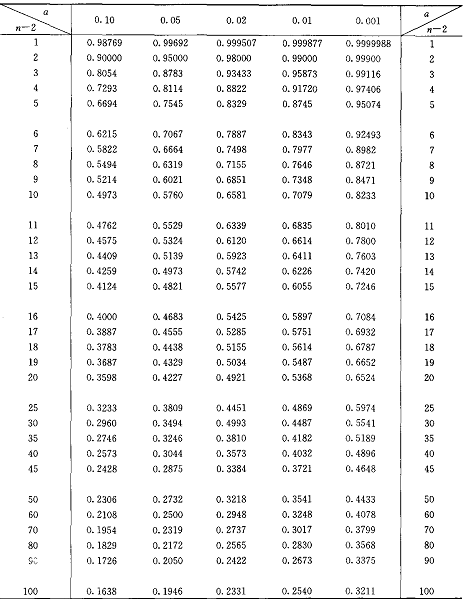
根据样本量30、选择α＝0.05的要求查表1-12得相关系数0.3494，而计算出相关系数为-0.851，判定是跑步时间与摄氧量负相关。

表1-12 相关系数检验表

P（｜r｜>r）=α

（五）散布图、相关分析法在应用中常见的问题

（1）对于散布图上出现的异常点，未经查明原因任意剔除。

（2）利用软件计算相关系数后，未经进一步的检验就判断变量之间是否相关。

（3）数据的收集未注意在相同条件下进行，易于造成判断失误。