简单平均法，就是利用过去的各期数据采用平均计算的方式，得到的平均值来作为下一期的预测值。计算公式是

预测对象预测值＝预测对象以往若干期历史数据之和／期数

比如利用2019年全年的月需求数据，通过计算每月的平均值，并把2019年的月平均值作为2020年1月的预测值。如图4-6，平均值4939就是作为下一期，即2020年1月的预测值。

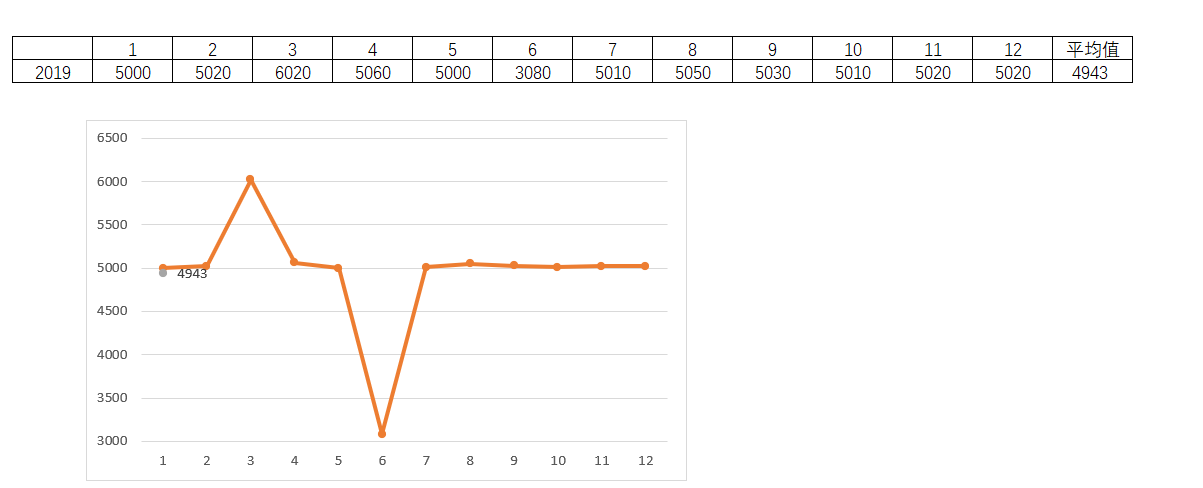
图4-6 简单平均法

简单平均法最大的优势就是通过平均的方式，消除了起伏的波动，当中包含难以剔除出来的噪声，当然如果没有进行事前的数据清晰，这个平均过程，同样也会把季节性因素，趋势因素等带来的波动起伏，一并进行削弱。这样的好处和不利处各有，有些偶发性的因素不会在未来重新反映，这样平均而减少波动影响，自然对预测带来好处，另一方面，有些因素是规律性的，会在未来不断重复反映，而时间序列技术，就是把过去规律重新应用在未来上，把这种因素带来的波动抹去，那么某种意义上就让预测变得失去规律。

简单平均法在需求稳定的情况下预测是比较准确的，比如在XYZ分类的X类，表现平稳，那么采用简单平均法会得到比较好的预测效果。

简单平均法一般来说，累积过去的数据，这样随着数据量的累积，平均值会变得不贴近实际，甚至可以形容为迟钝，从而变得不太可靠。

表4-5中回顾过去36个月的历史数据，并且以此这些数据的平均值作为下一期的预测值。同时再以过去12个月的历史数据的平均值来作为预测值，对比之下，使用36个月的历史数据计算的平均值，则和和最近的实际值不太贴合。

表4-5

2021年的实际需求多为7000个单位左右的水平，而2019年的实际需求多为5000个单位左右的水平，2020年则提升到6000个单位左右。从2019年5000个单位左右的需求水平，大幅度提升到2021年的7000个单位左右，不过作为预测值的平均值仅仅增长到6000个单位左右，预测具备滞后性。

采用全部数据进行预测的时候，时间历经越久的数据往往对现状就越不敏感，这种数据会让预测值滞后于实际状况。而且，预测的一个重要观点就是距离现在时间越近的数据越能反映现状。为此，有些时候采用简单平均法，就需要舍弃相当一部分的“陈旧”数据，截取最近的数据来进行预测，从而避免受到旧有信息的影响。如例中，选取了2021年的全年数据，因为其数据较新，对于用作2022年的预测，具有相当的参考意义。

这种做法固然能够克服“陈旧”数据的影响，不过截取哪一段时间的数据作为计算依据，是一个不容易的抉择。

还有一个值得注意的问题是，如果数据具备趋势和季节性因素，平均法并非一个较好的选择，因为它会抹去这些可以应用到未来的波动因素。