应用蒙特卡罗模拟是有前提条件的，那就是各变量之间的关系必须是独立的，某项作业的作业量变化与其他作业的作业量无关。如果彼此之间不是独立的，某项作业的作业量变化将带来其他作业的作业量的相应变化，就不能采用蒙特卡罗模拟，而应采用联合概率分析。

例如，A、B、C、D四项作业的作业量关系如图7-13所示。

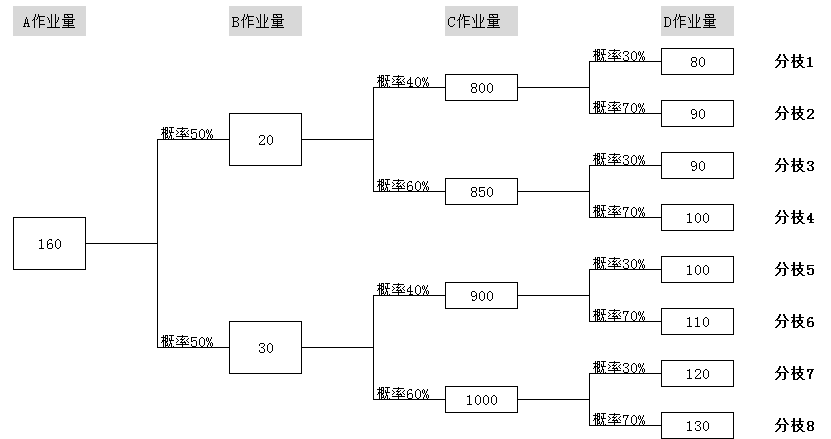
图7-13 各作业的作业量关系

对于分枝1：

利润=4×160+3×20+2×800+5×80-1000=1700元

概率=50%×40%×30%=6%

对于分枝2：

利润=4×160+3×20+2×800+5×90-1000=1750元

概率=50%×40%×70%=14%

对于分枝3：

利润=4×160+3×20+2×850+5×90-1000=1850元

概率=50%×60%×30%=9%

对于分枝4：

利润=4×160+3×20+2×850+5×100-1000=1900元

概率=50%×60%×70%=21%

对于分枝5：

利润=4×160+3×30+2×900+5×100-1000=2030元

概率=50%×40%×30%=6%

对于分枝6：

利润=4×160+3×30+2×900+5×110-1000=2080元

概率=50%×40%×70%=14%

对于分枝7：

利润=4×160+3×30+2×1000+5×120-1000=2330元

概率=50%×60%×30%=9%

对于分枝8：

利润=4×160+3×30+2×1000+5×130-1000=2380元

概率=50%×60%×70%=21%

如果也计算一下期望值，则：

期望值=各分枝的利润值×概率

=1700×6%+1750×14%+1850×9%+1900×21%+2030×6%+2080×14%+2330×9%+2380×21%

=2035

可以看到，联合概率分析介乎期望值法和蒙特卡罗模拟之间，期望值法给出唯一个预测结果，蒙特卡罗模拟理论上给出无数个预测结果及相应概率，联合概率分析给出多个预测结果及相应概率。