平均值在库存管理，计划管理中起着重要的作用，比如在不少公式的应用背景，都涉及正态分布，也叫高斯分布。这个分布的重点就是关注平均水平，而把意外当作是极端问题。

我们熟知的平均值实际上为算术平均值，除此之外还有几何平均值和调和平均值等。算术平均值就是把所有数字加起来，然后除以数字个数。在统计学上，这个算出来的值叫做均值，符号为，它是一个希腊字母，读作“缪“。

公式记为

表示的是所有数字的集合，n指的是数字个数。

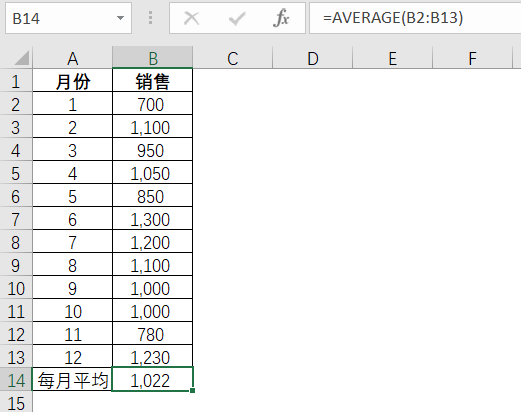
均值的计算在EXCEL可以通过average函数，快速地得出结果。如下某公司过去12个月的月销售量，根据相关函数就可以计算出平均每月的销售量。

表3-1 平均值在Excel的计算

在库存管理上，时间过于长久的历史数据并不足以信服用作参考数据，那么分配权重，对于时间远近作出合理的分配，越接近现在的数据越值得信赖的话，对此要把全部数据利用并算出均值，加权平均值就是需要计算的结果。

其公式为

其中表示各数字乘以对应的权重后，再求和。而表示权重之和。

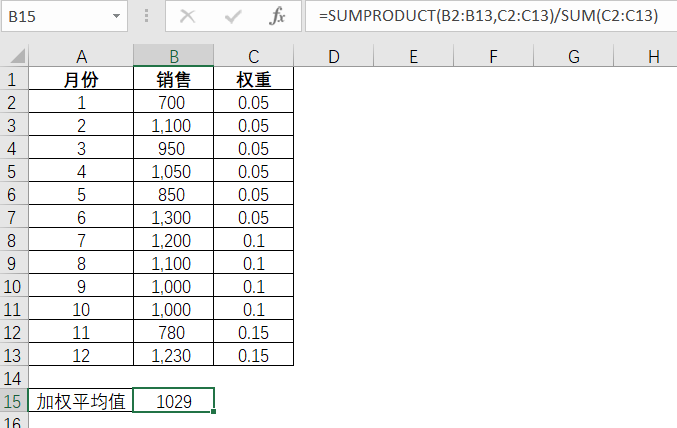
某公司的过去12个月的月销售数字，根据发生时间的远近赋予不同的权重，前6个月权重均为0.05，接下来的4个月为0.1，而最近的2个月权重则为0.15，权重合计为1。这些通过Excel函数sumproduct和sum可以快捷地求出加权平均值。

表3-2 加权平均值在Excel的计算

·

均值是一组常规样本大概率上最有代表性的统计量。比如哪一队篮球队正选地身高会更高一些，哪一个仓库中放置的库存时间更长一些，可以通过了解均值，借此了解其整体情况。

不过均值却是“坏家伙“，它经常骗了不少人。

2021年全国各省税前平均工资公布的时候，不少人的朋友圈都是满满地吐槽，都是那么一句：拖后腿了。

表3-3

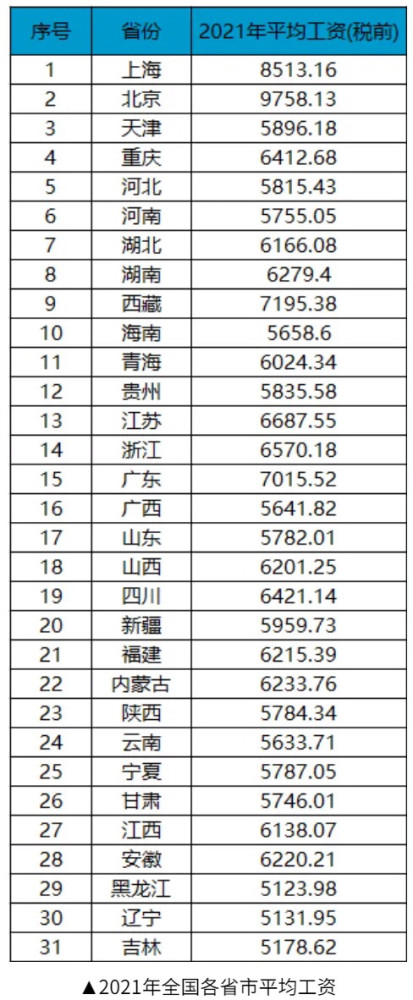
（数据来源于网络）

一心要追上平均工资的员工，莫不抱着“给我涨工资”的心态，提出诉求。

然而老板们一脸冷漠的表情，反驳道：“身在福中不知福啊！国务院总理说了，我国还有6亿人月入不足1000元，你比那6亿人好多了！”

然而事实上真的有那么多高工资的还是如国务院所指出的，尚有6亿人月入不足1000元？

均值只是大概率上反映了整体情况，那是因为其样本有着特殊情况，并不能反映样本数据的真实特征。当一些特殊的数据，即非常高的工资收入纳入计算样本中，那么最终得出的均值就无法描述整体的真实情况。

引入中位数，众数作为参考值，联同均值，从而更加清晰地了解整体的真实情况。

中位数是样本升序排列后最中间的数值。根据数据个数的不同，计算方法分为两种。

当数据个数为奇数时，中位数即最中间的数，如果有N个数，则中间数的位置为(N+1)/2，比如最近5天的销售数据为10，20，30，40，50 ，那么中位数就是按大小排序后最中间的数值。由于是5天的数据，最中间的数值就是（5+1）/2=3，排序的第三位数值就是30了。

当数据个数为偶数时，中位数为中间两个数的平均值，中间位置的算法是(N+1)/2。比如最近5天的销售数据为10，20，30，40，50，60，由于是6组数据，其中间位置就是（6+1）/2=3.5，即排序后的第三位和第四位的中间，也就是这两个数值的平均值。因此就是（30+40）/2=35了。

均值容易受到特殊数值的影响，而中位数则不会，相对地客观反映出整体的情况。

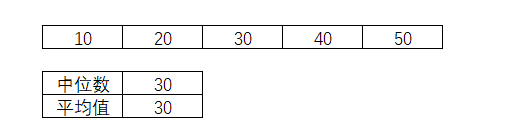
刚才的5天销售数据，通过计算得出中位数和均值，都是30。

表3-4 平均值和中位数

如果再加入前一期的销售数据500，然而这个数据非常大，和这5者数据有着明显的差异，由此而得出的中位数和平均值也相应地变化。

表3-5平均值和中位数

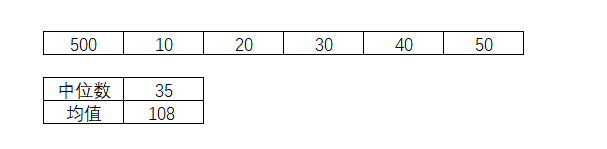
均值因为这个特殊的数据加入，产生了较大的变化，并且得出的结果，和这6个数据并没有任何相对的接近。而中位数则差不多。中位数的计算，是和每个数据的位置有关系，即使有极端的特殊值加入，都是排序在旁边的位置，而不会加插在中间。对于求中间位置数值的中位数而言，这样的特殊值不会造成太大的影响，那么在无法利用均值很好地反映整体情况下，中位数可以给予重要的参照。

众数是指出现次数最大的那个数值。

表3-6平均值，中位数和众数

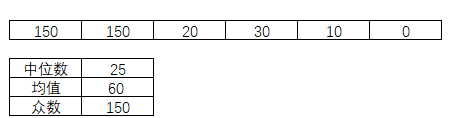
众数能够反映数据样本的局部特征。如果不清楚图3-7中6组数据的每一个，那么通过中位数，均值，众数，清楚明白到由于相当数量的数值150，从而使得处于多数的小数值被拉动，令到均值为60，但是中位数只是25。

均值，中位数，众数，加上最大值和最小值的话，就可以帮助抹除掩盖数据的重重遮挡，有利于清楚数据的全貌，从而避免被部分展现的数据欺骗。

当能得知工资数据的各种情况时，就容易明白，很多时候并非你拖了平均工资的后腿，而是高工资的那些，工资值太高了，拉高了平均数值而已。