指数平滑法，面临最大的问题就是如何选择适合的指数参数。尽管在前文提到因应不同的情况，选择不同的指数参数范围，不过确立了范围，从中寻找适合的参数值，也并非一件容易的事情。比如单指数平滑法，只有一个指数参数α，那么可以通过选择不同的参数来尝试，直接得到理想的拟合度。但是一旦遇上三指数平滑，要不断调整三个参数的话，花费的时间就比较多，操作也麻烦。因此，Excel的规划求解可以有效地提供帮助。

确立适合的参数，就是让预测和实际的模型拟合度尽可能地高，而误差等指标可以给与有效的帮助。

四个基本的指标，误差，绝对误差，误差平方，以及绝对误差百分比，对于后续的参数选择起着重要的指示作用。

对相关期数的实际值和预测值进行误差等的计算，得到相关的数据值。

表4-36

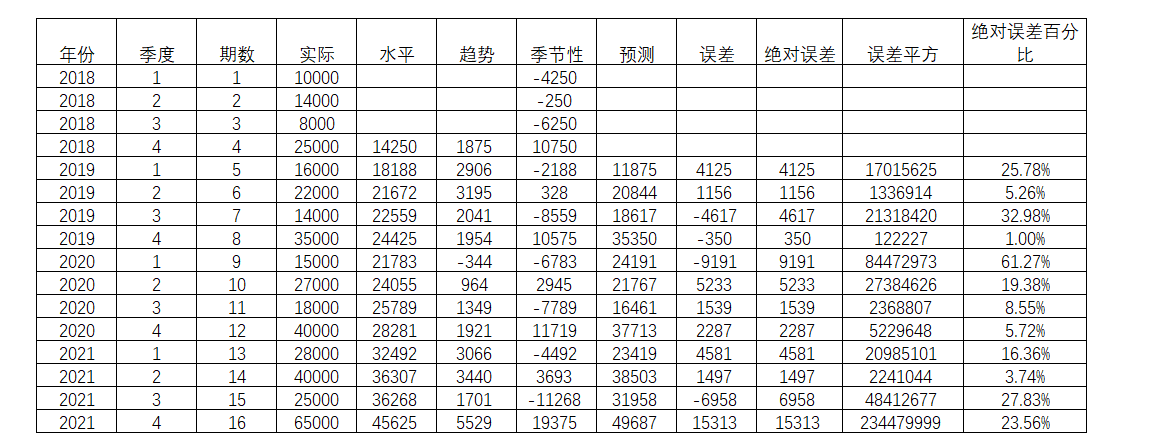
接着对绝对误差，误差平方，绝对误差百分比进行平均，得到对应的平均值，分别是MAE（Mean Absolute Error，平均绝对误差），MSE（Mean Squared Error,平均平方误差）以及MAPE（Mean Absolute Percentage Error, 平均绝对百分比误差）。并且相应的三个参数α，β和γ分别是0.5，0.5和0.5。由此得出的MAE，MSE和MAPE值分别为4737，38780672和19.29%。

表4-37

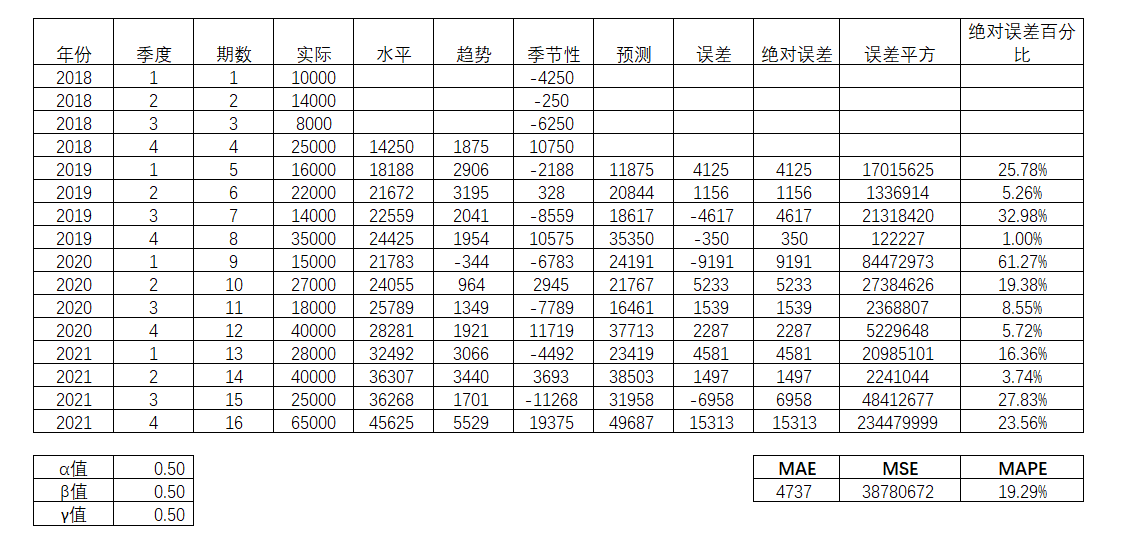
Excel的规划求解有助于通过最小化其中一个数据，诸如MAE,MSE又或者MAPE,然后借此找到适合的参数。Excel-数据-规划求解，可以快速地帮助确立三个适合的参数。当决定以最小化MSE，那么添加相应的约束条件，即α，β和γ三个指数都在0和1之间。

表4-38

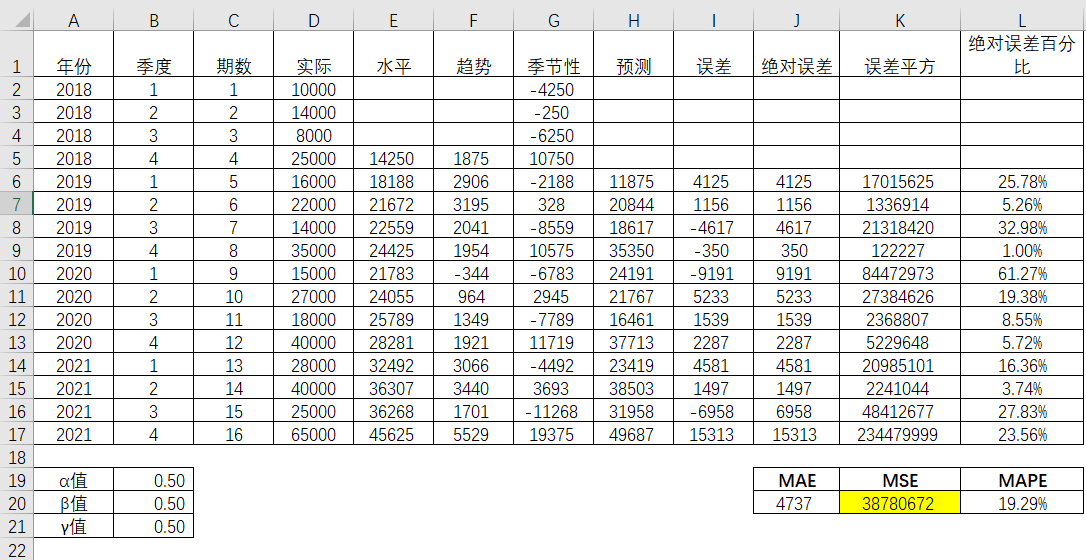
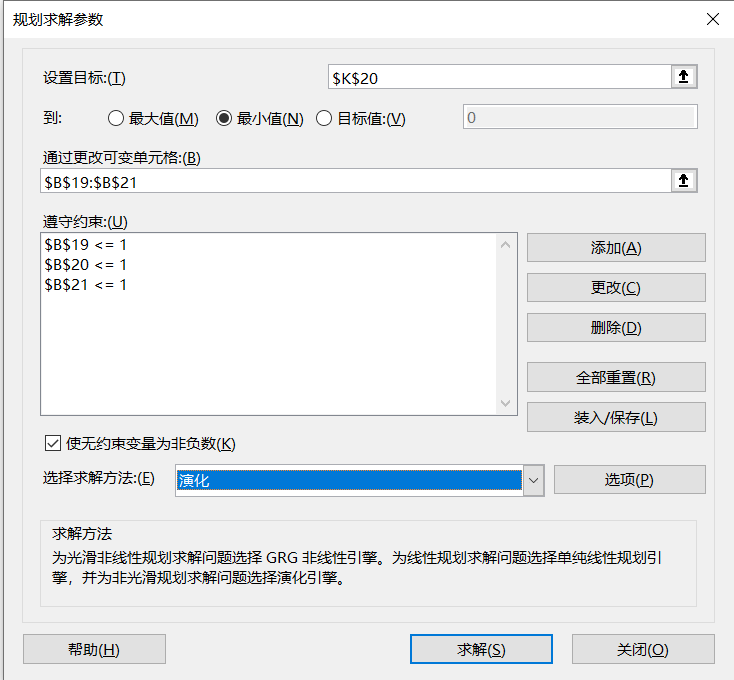
图4-25

在选择求解方法上，选择优化。求解方法共有三种，分别为非线性GRG，单纯线性规划和演化。单纯线性规划是用于线性问题，在这里并不适合。至于非线性GRG，是常见的非线性规划求解方法，不过得到了局部的最优解，就停止了搜索，继续探究下去。这个最优解可能是全局最优解，也可能不是。因此可能也会出现下图情况，计算到了局部最优解就停止了，而没有继续下去，计算到全局最优解。

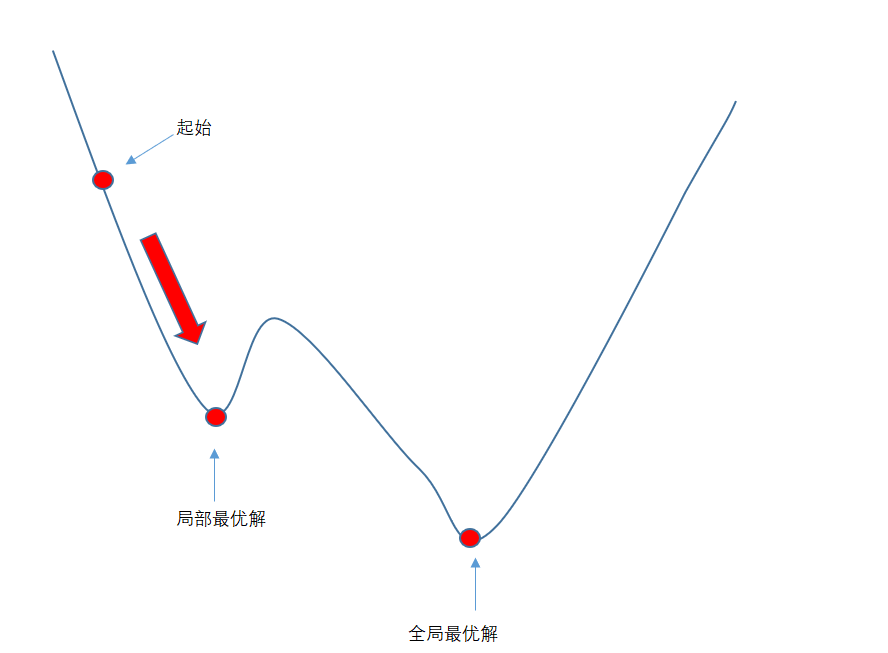
图4-26 局部最优解和全局最优解

至于演化算法，则是用一些随机数(在用户定义的变量范围), 代入到模型, 不断循环迭代, 直到目标函数长时间没有进一步收敛(减少或增加), 则停止迭代的求解. 这是一种探索式和随机式求解的结合, 很多时候可以找到全局最优解。因此选择使用演化算法。如果对此没有把握，也推荐三种方法分别尝试，进行对比，寻求最小化的MSE数值。

完成规划求解之后，得出新的三个参数，α值为0.02，β值为1.00和γ值为0.23。确立这三个参数之后，MSE值达到最小化，为33865391。那么可以根据这三个参数进行后续期数的预测。除此之外，最小化MAE, MAPE等其他数值，以此求得适合的参数，可以根据实际情况和需要进行选择，以及比较。

表4-39

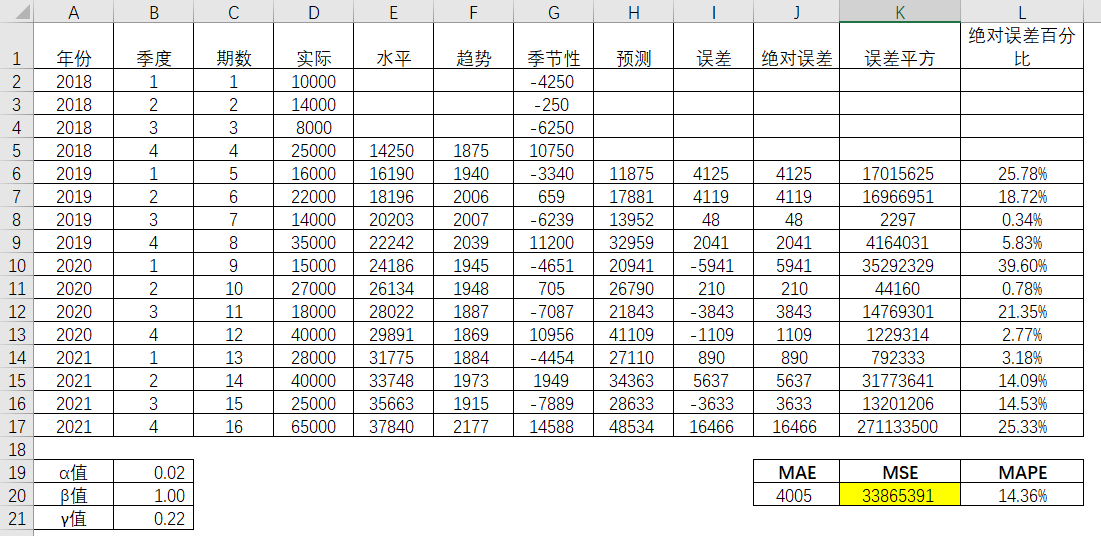
通过对比，规划求解后的模型的趋势来看，预测的走向和实际的走向更加贴切，特别是第9期到第11期的变动，拟合度显得更加高。

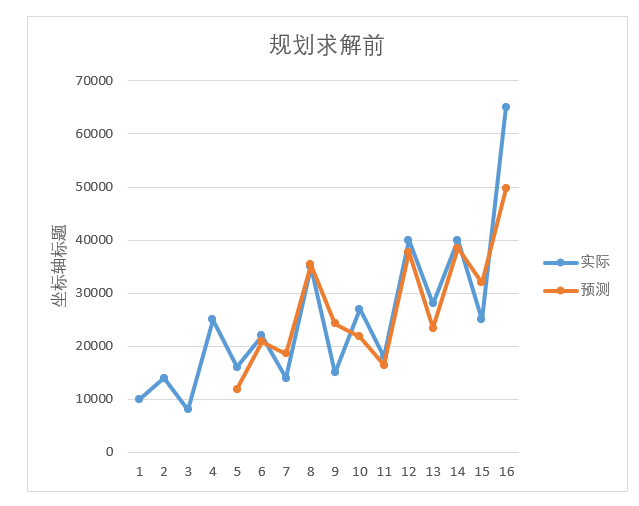
图4-27

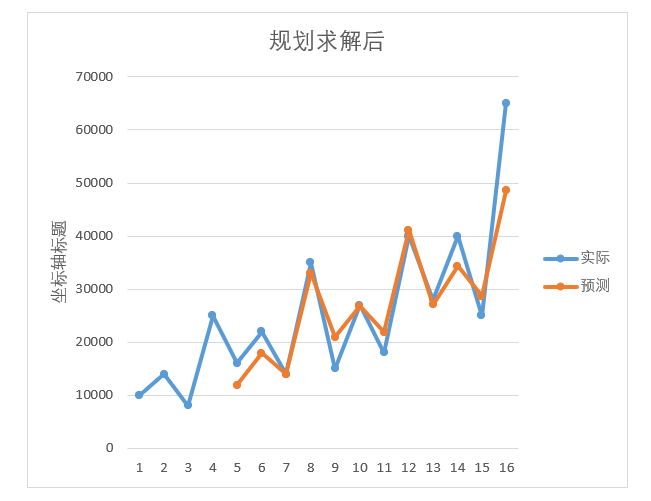
图4-28

【小插曲3】跟踪信号能干什么

跟踪信号（TS，Tracking Signal）是指预测误差滚动和和与平均绝对偏差的比值。是用来衡量预测的准确程度的。当预测每周、每月或每季都更新时，将新的已获得的实际需求量与相应预测值比较。一般认为此数据高于6或者低于-6，需求会被认为高估或者低估，最理想的值为0。而这个也表明所使用的预测方法不适合或者潜在需求模式发生了变化。

当需求突然减少或急剧增加使得历史的数据没有任何借鉴意义，跟踪信号可能会变得相当大，这就提醒我们需要改变预测方法或者注意权重的分配。

跟踪信号的计算公式

MAD是指Mean Absolute Deviation，称为平均绝对偏差，它是指各个变量值同平均数的离差。计算方法比较简单，先计算实际值的平均值，然后再得出各实际值和该平均值之差的绝对值，最后计算这些绝对值的平均值就可得出结果了。

首先从各期实际值中得出平均值。

表4-40 各期平均值求解

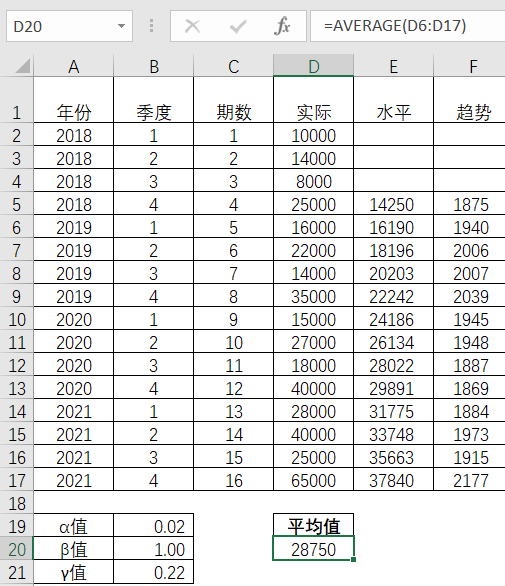
接着计算各期的绝对偏差值。

表4-41 各期绝对偏差值求解

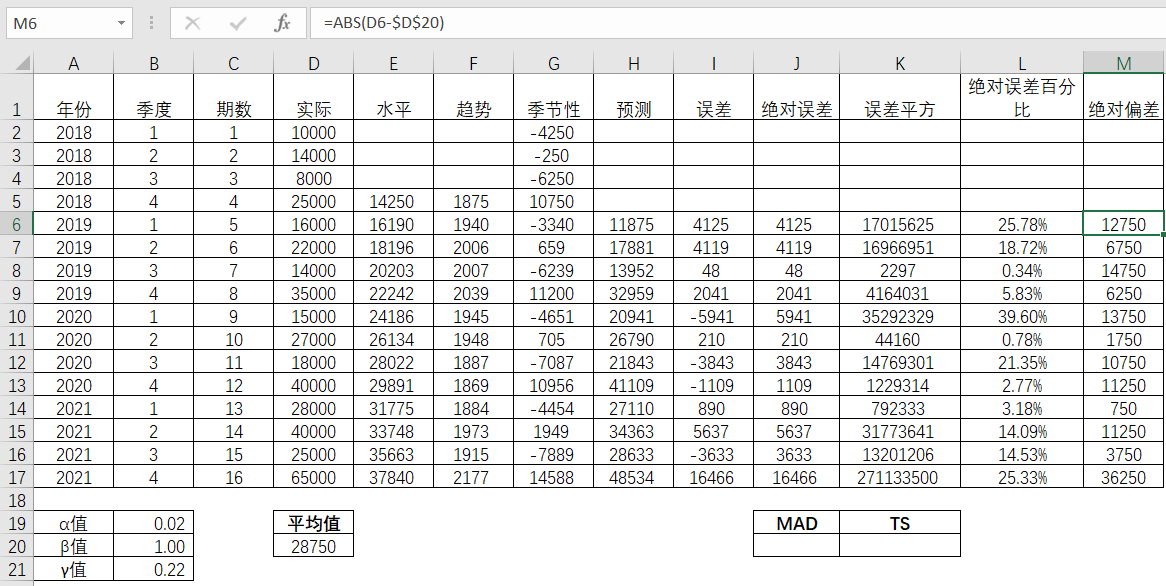
那么就最后就得出MAD值了。

表4-42 MAD值求解

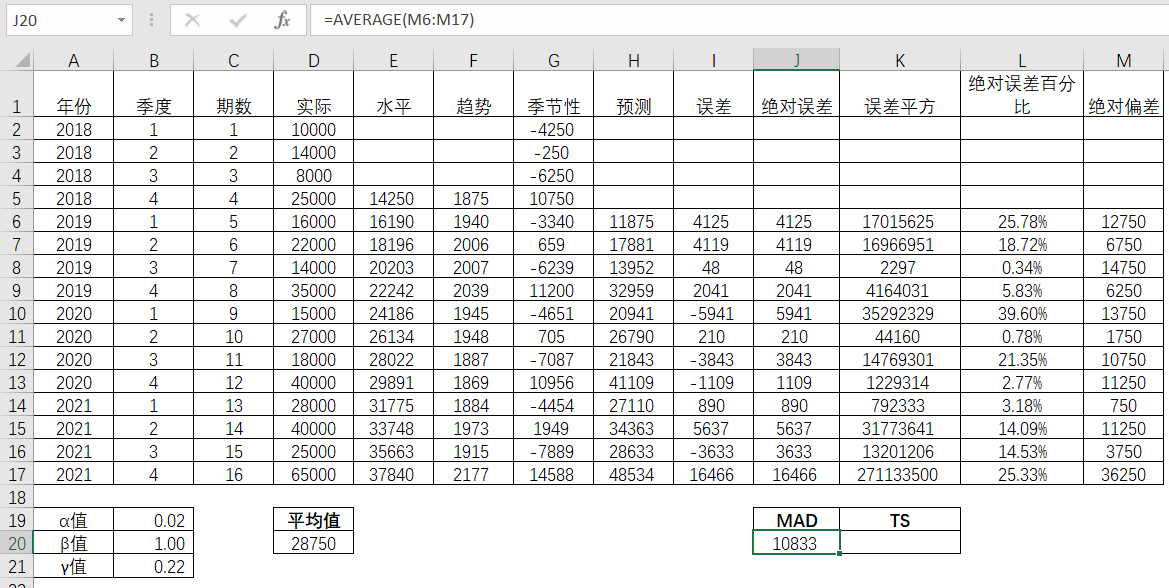
最后有了各期的实际值和预测值之差的绝对值，以及MAD，那么TS就可以通过公式计算出来了。TS为4，属于可接受范围内。这个正值为4的信号表示，实际需求大于预测值。反之，若是结果为负，则表明预测值大于实际值。

表4-43 TS值求解

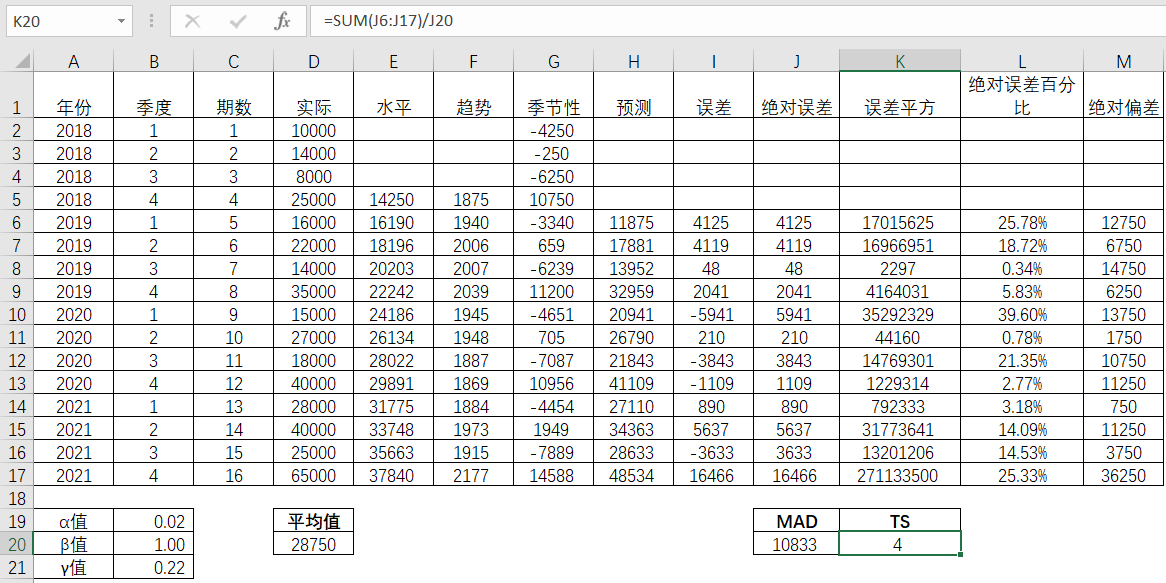
在计算TS的时候，有些说法是MAD的计算方法等同于MAE（平均绝对误差），也就是把绝对误差的平均值作为计算的分母。在英文含义上，MAD的D（Deviation）和MAE的E（Error）某种程度上视为相同，因此MAD的计算也视同MAE的计算。在现实操作上，把MAE作为分母计算也得到广泛的应用。

不过实际上，MAD是表示各个变量值之间差异程度的数值，它的表示范围比MAE更广泛些，在计算上，除了可以计算各变量和平均值的离差，也可以选择中位数或众数来取代平均值作为计算依据。本例中只采用了平均值作为计算MAD的依据。