（一）集中程度分析

1．平均数

平均数即指标的平均水平。例如，客户、产品、作业、部门等多维组合的成本对象有100万个，总成本1000万元，则：

平均数=1000÷100=10

2．中位数

众多的成本对象，小于中位数的占一半，大于中位数的占一半。例如，客户、产品、作业、部门等多维组合的成本对象有100万个，成本的中位数为10元。即100万个成本对象中，成本大于10元的有50万个，成本小于10元的也有50万个。

3．众数

众数是成本指标最普遍出现的值。例如，客户、产品、作业、部门等多维组合的成本对象有100万个，成本为10元的有8万个，数量最多，则成本的众数为10元。

（二）离散程度分析

1．极差

即成本指标的最大值与最小值之差。例如，客户、产品、作业、部门等多维组合的成本对象有100万个，成本最大的为88元，最小的为33元，则：

极差=88-33=55元。

2．四分位差

它是剔除1/4最大指标和1/4最小指标的成本对象后，剩余对象的极差除以2。例如，客户、产品、作业、部门等多维组合的成本对象有100万个，剔除25万个成本最大和25万个成本最小的成本对象，剩余50万个成本对象成本最大的为66元，最小的为44元，则：

四分位差=66-44=22元。

3．平均差

即各成本对象的成本指标与平均数的差额的绝对值的平均数。例如，从客户、产品等维度组合中选择5个分析对象，成本分别为8、9、10、11、12，则：

平均数=（8+9+10+11+12）÷5=10

平均差=（|8-10|+|9-10|+|10-10|+|11-10|+|12-10|）÷5=1.2

4．方差

即各成本对象的成本指标与平均数的差额的平方的平均数。例如，从客户、产品等维度组合中选择5个分析对象，成本分别为8、9、10、11、12，则：

平均数=（8+9+10+11+12）÷5=10

方差=（（8-10）2+（9-10）2+（10-10）2+（11-10）2+（12-10）2）÷5=2

5。标准差

即方差的平方根。例如，从客户、产品等维度组合中选择5个分析对象，方差为2，则：

标准差=20.5=1.414。

6．变异系数

即标准差除以平均数。例如，从客户、产品等维度组合中选择5个分析对象，标准差为1.414，平均数为10，则：

变异系数=1.414÷10×100%=14.14%。

（三）斜尖程度分析

1．偏度

即对象指标的不对称水平，用于衡量分布的偏斜程度，等于三阶中心动差除以标准差三次方。三阶中心动差，等于各对象指标与平均数的差额的三次方的平均数。

例如，从客户、产品等维度组合中选择5个分析对象，如果成本分别为8、9、10、21、12，则：

平均数=（8+9+10+21+12）÷5=12

三阶中心动差=（（8-12）3+（9-12）3+（10-12）3+（21-12）3+（12-12）3）÷5=126

方差=（（8-12）2+（9-12）2+（10-12）2+（21-12）2+（12-12）2）÷5=22

标准差=220.5=4.69

偏度=126÷4.693=1.221

偏度大于0代表正偏斜，如图7-1所示。

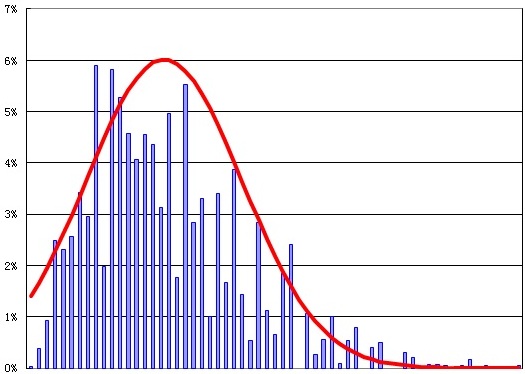
图7-1 偏度大于零

再如从客户、产品等维度组合中选择5个分析对象，如果成本分别为8、9、10、11、12，则：

平均数=（8+9+10+11+12）÷5=10

三阶中心动差=（（8-10）3+（9-10）3+（10-10）3+（11-10）3+（12-10）3）÷5=0

偏度=0

偏度等于0代表正态分布，如图7-2所示。

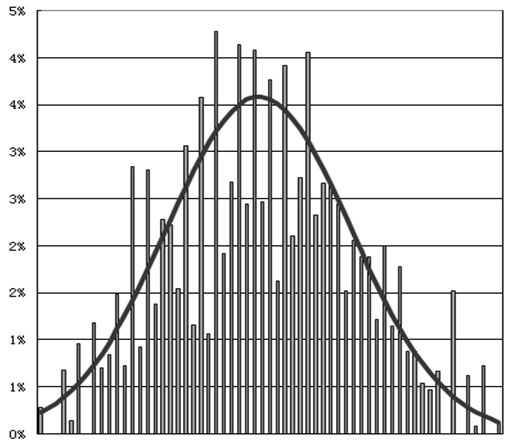
图7-2 偏度等于零

再如从客户、产品等维度组合中选择5个分析对象，如果成本分别为1、6、10、11、12，则：

平均数=（1+6+10+11+12）÷5=8

三阶中心动差=（（1-8）3+（6-8）3+（10-8）3+（11-8）3+（12-8）3）÷5=-50.4

方差=（（1-8）2+（6-8）2+（10-8）2+（11-8）2+（12-8）2）÷5=16.4

标准差=16.40.5=4.05

偏度=-50.4÷4.053=-0.759

偏度小于0代表负偏斜，如图7-3所示。

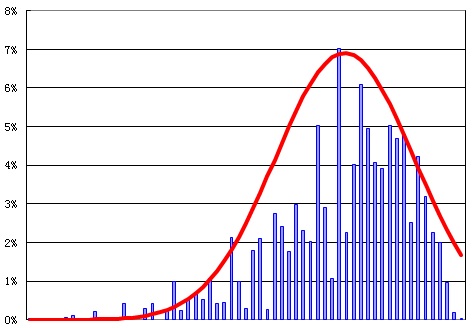
图7-3 偏度小于零

2.峰度

即对象指标的集中水平，用于衡量分布的尖峭程度，等于四阶中心动差除以标准差四次方再减3。四阶中心动差，等于各对象指标与平均数的差额的四次方的平均数。

例如，从客户、产品等维度组合中选择5个分析对象，如果成本分别为8、9、100、11、12，则：

平均数=（8+9+100+11+12）÷5=28

四阶中心动差=（（8-28）4+（9-28）4+（100-28）4+（11-28）4+（12-28）4）÷5=5462647

方差=（（8-28）2+（9-28）2+（100-28）2+（11-28）2+（12-28）2）÷5=1298

标准差=12980.5=36.03

峰度=5462647÷36.034-3=0.242

峰度大于0表示分布比正态分布更集中，呈尖峰状，如图7-4所示。

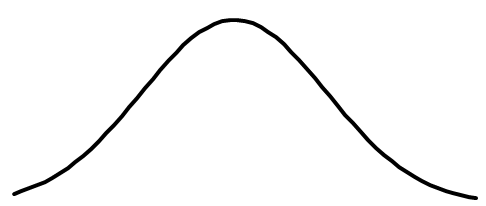
图7-4 峰度大于零

再如，从客户、产品等维度组合中选择5个分析对象，如果成本分别为8、9、10、11、12，则：

平均数=（8+9+10+11+12）÷5=10

四阶中心动差=（（8-10）4+（9-10）4+（10-10）4+（11-10）4+（12-10）4）÷5=6.8

方差=（（8-10）2+（9-10）2+（10-10）2+（11-10）2+（12-10）2）÷5=2

标准差=20.5=1.414

峰度=6.8÷1.4144-3=-1.3

峰度小于0表示分布比正态分布更分散，呈平坦状，如图7-5所示。

图7-5 峰度小于零

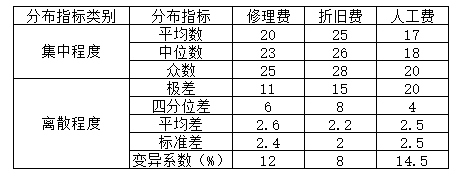
分布分析可以结合比较、趋势等分析，例如对于选择的众多成本对象，可以计算各类成本项目的各类分布指标，如表7-1所示。

表7-1 各类成本项目的各分布指标

基于成本项目的分布指标，可进行比较、趋势等分析，如图7-6所示。

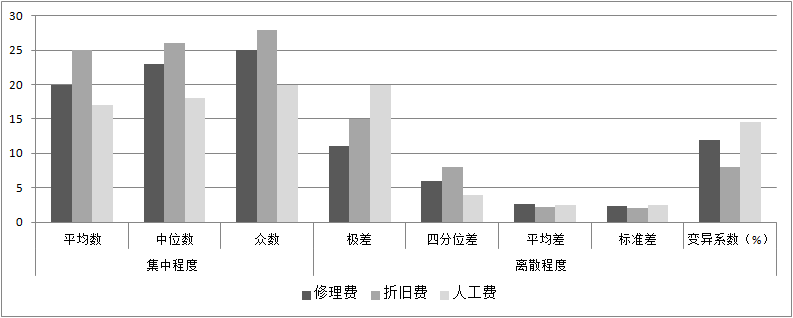
图7-6 成本项目的分布指标比较分析

在进行分布分析时，我们可以针对关注的重点，选择或大或小的成本对象范围，选择或多或少的成本项目。可供选择的成本对象数量很多，成本项目很多，总的来说计算工作量很大，不仅对算法要求高，而且对性能要求高。对于这把深度挖掘数据特征的瑞士军刀，我们可以不去掌握它的加工过程，但至少要知道它的应用场景和业务意义。