XYZ反映货物波动特征，起着很重要的货物需求指示作用。而ABC分类则标识了货物对待程度的区别程度，两者结合就更加有助于我们制定库存策略。

货物价值和需求变动的结合，形成了九种货物特性。诸如AX，BY之类等。针对不同特征，因材施法。

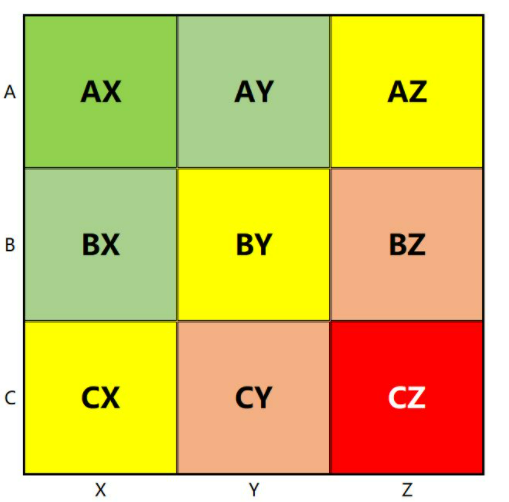
图2-7 ABC-XYZ九宫格

每一种组合代表着一种特性，下图是对这九种组合特性的说明。

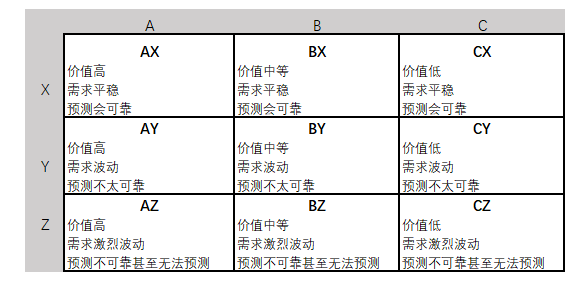
图2-8 ABC-XYZ结合特征表现

如果产品是AX，则它们需求非常稳定，并且库存价值较高，因此避免持有大量库存，减少资金积压在库存上，同时稳定需求的情况下，可以设立计算机定期自动订货处理，人工干预为辅。

而产品为AY或BX时，虽然AY的库存价值较高，不过需求处于一定的波动，但属于可以控制风险，因此可以参考过去需求的平均值来持有备货库存，不过库存价值高，注意减少备货量的同时，也要认识到由此存在的缺货风险。同样BX库存价值相对低一点，需求平稳，也可以参照过去需求平均值来备货，库存量不需要考虑备太多，足够和一定程度上安全保证供应即可。两者也可以设立自动订货，

AZ类型的货物，价值昂贵但需求不稳定，可以通过共识的订货点上来进行连续的小批量订货以应对，从而减少库存的持有避免占用更多的资金，甚至更进一步为了资金考虑，仅根据订单来备货，并让客户明白和接受备货的提前期。BY也可以采用类似的策略，考虑到库存价值相对低一点，需求也较平稳一点，订货的数量和库存持有量根据波动特征，例如季节性等适当增加。对于CX需求平稳，价值不高，采用双堆法。

BZ的产品类型，即需求不确定，需要更大的库存覆盖率。一个有用的经验法则是采用定量订货，当库存降低到一个位置的时候，订购到某个得出共识的最大库存点。至于CY类型产品，库存价值低且具有可控制的风险，设立需要较小的库存覆盖率来满足需求。

最后，代是CZ产品，其存在积压的高风险，尤其是不要在这些产品上放置过多库存甚至根本不放置任何库存，只要按照订单备货。

除此之外，还可以根据这9种不同特征，设立不同的库存持有天数限制，从而对该类性的SKU进行有效的库存管理。比如AX的库存持有天数限制值设立在10天，而AY则设立在15天。

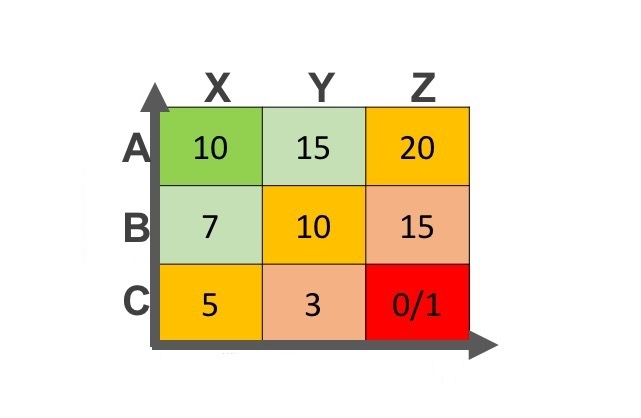
图2-9 ABC-XYZ分类的各自持有库存天数

【小插曲】洞中窥天，能见全貌？从样本推算总体

标准差是衡量一组数据的离散程度。我们可以通常利用Excel函数来帮助计算。不过函数却有两组，分别是stdev.p和stdev.s。同一组数据，分别标记为A组和B组，两个函数计算出来的标准差结果却是不相同。

表2-7 标准差计算差异

A组数据，使用stdev.p来计算，结果是196.65；B组数据，使用stdev.s，结果是205.40。

标准差的计算，是方差的开方。方差是一组数据，数值与均值的偏离程度。

当手头拥有一组数据，并且知道这组数据的全部，那么它的方差公式如下

其中

：总体方差 ：总体均值 ：样本大小

但是即使手头拥有一组数据，只是知道这组数据里的某部分而非全部，那么在这里是无法计算出该组数据的方差，而只能通过所知道的有限数据而估算这组的总体方差。其公式就是

：样本方差 ：样本均值 ：样本大小

在这里，方差不再用表示，而是用来表示其是样本的方差，和这个总体方差以作区别。至于用样本n减去1，因为它不是计算，而是利用已知的部分样本数据来估计整体的方差，为了估计得更准确一些，除数用了n-1，而不是n，这样的出来的结果会略大一些。

使用除以n-1计算的这个公式经过证明，在任何时候都是能够得到比较接总体标准差的结果，这就是所说的无偏估计。用数学的说法就是：这个估计值与正值之间的误差是收敛的。用通俗的话说，就是这个估计值比较靠谱。

数学上讲，当n越大时，这个估计值就越接近真值。实际意义就是，样本数量越大，就越能代表总体。

那么总体标准差的公式如下

在Excel中就是函数stdev.p，用以计算整体数据的标准差。如上例A组，12个数据就是整组数据的全部，那么就因此计算出这一组的标准差。

而样本标准差的公式如下

在Excel中就是函数stdev.s，用以估算总体数据的标准差。如上例B组，12个数据只是其中一部分数据，并不知道全部数据，因此通过这12个样本数据来估算出总体的标准差。

按照中心极限定理，样本平均值约等于总体平均值，且不管总体是什么分布，任意一个总体的样本平均值都会围绕在总体的平均值周围，并且接近正态分布。

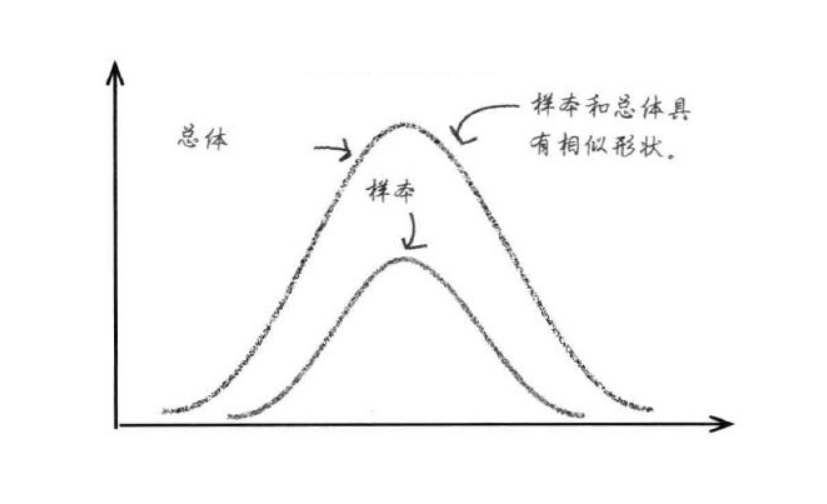
图2-10 样本与总体分布的表示

一般现实处理上，我们获得总体样本的所有数据来处理库存等的机会很大，那么使用总体计算标准差自然更为适宜。另外无论是用stdev.p还是stdev.s函数计算标准差，从而得出变异系数和XYZ分类，这个结果的差异并非大得无法接受，而XYZ分类的重点在于区间的划分，而非过分着眼于计算的精确，那么即使都以stdev.p计算也无妨。