自主招生与数学竞赛中的函数问题与高考中的函数问题，在解题策略层面没有本质的区别，唯一有别的是可以使用特殊极限定义，特殊极限，例如，罗贝塔法则等，例如求的最小值．显然这是一个二元函数求最值问题，由于两个变量是独立的，所以可以先看作关于t的二次函数，求出最小值后，最小值又是关于x为变量的函数，一元函数的最值通法就是求导，这样问题便可顺利解决．

下面我们举几个自主招生与竞赛的函数题目，看看从解题策略方面两者的联系与区别．

例2-27（2015清华领军）已知函数，则

A.有极小值，但无最小值

B. 有极大值，但无最大值

C.若方程恰有一实数根，则

D. 若方程恰有三个不同得实数根，则

实际上本题只需要画出函数图像的草图即可，怎么画函数图像的草图呢？与高考中画函数图像草图的方法一样，从解析式中获得函数的定义域、对称性、零点、单调性、极值、渐近线、最值等几何特征即可画出图像草图了．

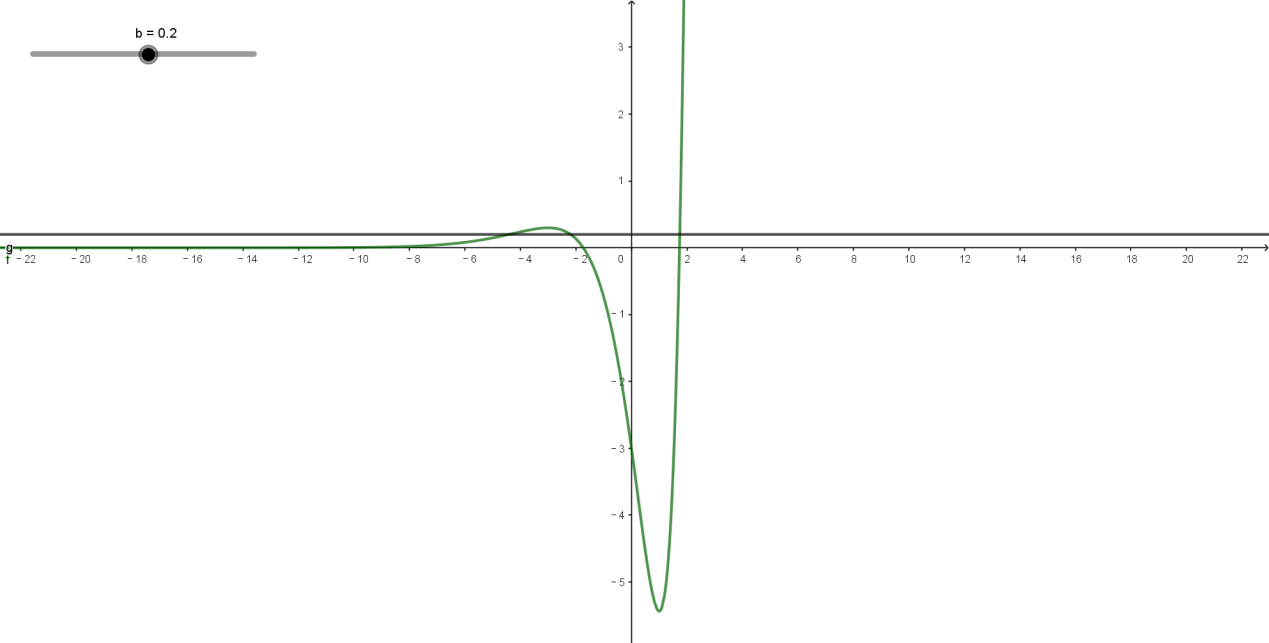
例2-28（2017北大特优考试）

为可导函数，，且．

下列结论正确的是

（A） （B） （C） （D）

分析：此题的基本思路是由已知的两个条件能推出四个答案中的哪一个答案是正确的，因此，关键是对和的认识．

在中，令，得，即，可见，试图由求出的解析式是不可能的．是什么意思呢？的结构，在分式求导中会出现，求导后出现原函数与导函数的差，说明说明有一个因子求导后与求导前是不变的，自然想到了函数，这样

等价于，

当时，，说明函数在上是递增的，所以，

又，所以．

例2-29（2015清华领军）已知非负实数满足，则的

A.最小值为 B. 最小值为 C.最大值为1 D.最大值为

这是一个有约束条件的二元函数最值问题，通法是利用，即将目标函数转化为一元函数，再用一元函数求导的方法加以解决，可想而知，作为选择题运算量还是比较大的．最为自主招生题，我们注意到已知条件和目标函数都具有明显的几何意义，已知条件是一条线段，目标函数的几何意义是线段上任意一点到y轴的距离与到原点的距离的和．由于原点是定点，直线也是确定的，设原点O关于直线对称的点为A，如图．

最小值时，D，C，A三点共线，最大值时，在线段的两个端点处．答案为A，C．

从这道题的解答可以看出，自主招生题并不像高考题那样注重通性通法，而更注重抽象代数形式的几何表达与文字语言的描述，也就是更注重数学对象本质的理解．

我们再看这样的几个例子：

例2-30（2015清华领军）

如图，已知直线与曲线相切于两点，则有

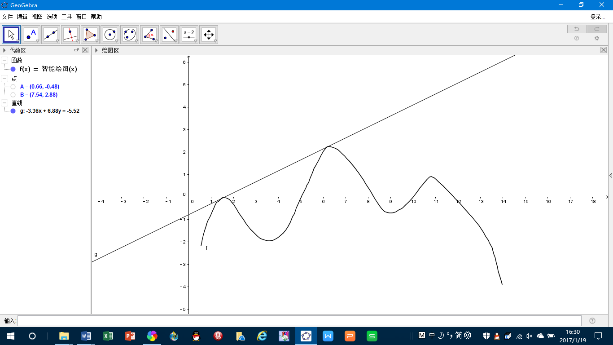
A．2个极大值点 B.3个极大值点 C.2个极小值点 D.3个极小值点

分析：函数有几个极值点，首先看导函数有几个零点，而

，，即，它的几何意义是，函数有几个点处切线斜率等于k，数形结合，共有五个点，而且这五个点都是函数的极值点．根据五个点两侧的正负变化，可得答案选BC．

此题的解答不再纠结于具体函数，而是注重对极值、导数等概念的本质理解．

例2-31（2015清华领军）设函数，则

A. B.

C.曲线存在对称轴 D. 曲线存在对称中心

分析：此问题的本质是研究函数的性质，由解析式可知，函数定义域为R，分子是三角函数，是其图像的一条对称轴，分母是二次函数，图像关于对称，这样整个函数就关于直线对称；又当二次函数取得最小值时，刚好取得最大值1，所以整个函数值；，我们知道，对于正弦函数，有一个重要不等关系，当时，，进而可得时，，即，由于为偶函数，且为周期是2的函数 ，当时，，当时，，，由周期性，时，，这样，．所以，答案A,B,C均正确．

例2-32（2011全国数学联赛一试）

若方程在上有唯一解，求的值．

分析：从本质上讲，这道题是要画出函数图像的草图，显然，这个函数表达式有进一步化简的余地，于是

设，

，

，

，

由此可得，函数是上的偶函数，周期为，关于直线对称

函数在上的零点，

函数在时取得最大值1．

进一步分析可知，函数图像关于直线对称．证明如下：

因为，

所以关于直线对称．

故在上有唯一解，只能或．

当时，，此时在上有5个解，不合题意舍去；

当时，，此时，

因为时， ，

所以且，得为唯一解 ．

所以．

例2-33 求所有的实根.

这是一道初中数学竞赛题，从表面看，这是关于x的超越方程，无法通过常规方法求解，但这个方程比较特殊，可以通过配方，形成平方和等于零的形式，从而求解．

但此题的另一种看似错误的解法，却引发了对二次方程判别式本质的认识．我们先看作法：

把方程看作关于x的二次方程，由已知方程有实根，所以，即，，又，所以，，在此条件下，原方程变为，经检验，均为原方程的解．

有人认为，这个方程不是二次方程，犯了概念性错误，这实际上是对判别式的误解，判别式只是一个记号，而它的本质是关于某个字母的二次方程经过配方以后右变非负的一种表达，我们简单回顾一下判别式的推到过程．

，

，

由于，所以

要使上面的方程有实数解，必须，即，

换句话说，要使在实数范围内有解，必有，

这里，可以是实数，也可以是字母，或是多项式，甚与有关的多项式，等等，这才是判别式的本质．所以，竞赛与自主招生更注重考查数学知识的本质．

例2-34 已知函数是连续的偶函数，且当时是严格单调函数，则满足的所有x之和是

（A） （B） （C） （D）

分析：这道题主要考查对函数奇偶性和单调性的理解，从几何直观的角度更容易找出解题思路．由知，，或，也就是，，

或，，所以．

例2-35函数的图像关于直线对称，据此可以推测，对任意的非零实数关于x的方程的解集都不可能是

（A） （B） （C） （D）

分析：这道题的关键是对条件“关于x的方程的解集”的理解，从宏观来看，这个方程首先是关于的二次方程，由于为任意非零实数，有可能只有一个值或两个值，若只有一个值，那么，x要么有一个值，或有两个关于直线对称的值，显然答案（A）（B）都有可能；若有两个值，那么，x要么三个值，有一个值，另外两个关于直线对称，要么四个值，两对都关于直线对称，从而，只有答案（C）才有可能．

由上述解答可以看出，理解二次函数的性质，二次方程与二次函数的关系等是顺利解决此问题的前提．

例2-36 关于x的方程①存在实数k，使得方程恰有2个不同的实数根；②存在实数k，使得方程恰有4个不同的实数根；③存在实数k，使得方程恰有5个不同的实数根；④存在实数k，使得方程恰有8个不同的实数根．其中假命题的个数是

．

分析：此题的关键是对方程的认识，如果换元，比如令，则方程为，

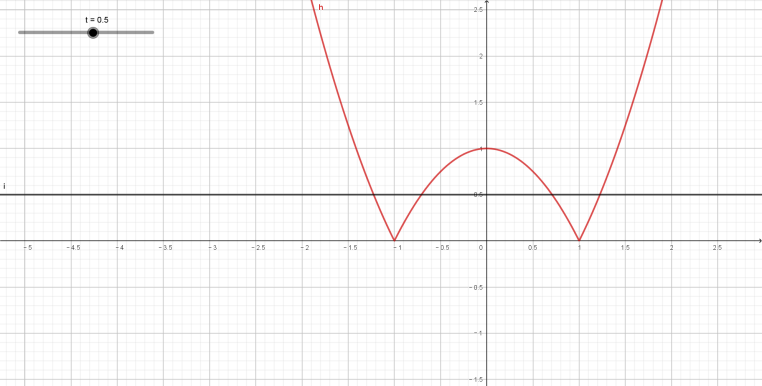
当时，，此时方程有4个根；当时，，此时方程有2个根；当时，，，此时方程有8个根；，方程5个根.因此，四个命题都正确．

例2-36已知函数在定义域内对任意恒满足，且，则 ．

分析：对于这类抽象函数问题，常用的解法是给赋值，从特殊到一般，找出其规律，从而作答，但如果我们是命题的人，这些题是怎么命制出来的呢？一定是有一个具体函数，所以，这类题目的另一种做法就是根据函数满足的性质构造一个具体函数，从而解答．

思路1：令，得，或，

若，又，令，，矛盾

所以，，，

由此可得，，，，

，，是周期为6的函数，

．

思路2：中学阶段学过的哪一个函数具有运算性质，我们一一梳理一下：

：

：

：

：

：

了解基本函数的运算性质及其结构特点，我们发现满足条件的函数是余弦型函数．

如何确定具体表达式呢？

尝试设，但，

为此修改为，

又知，将上式修改为，

所以．

可见，了解基本函数的运算性质对解决这类问题至关重要．

例2-37（2014北京大学自主招生）

已知，，，则等于

（A） 4027 （B）4028 （C）4029 （D）4030

思路1：赋值法

①，得；

②，得

③，得

解得，，猜想，则．

思路2：由于，另一方面，

所以，

所以，设，由，，解得，

思路3：也可以通过Jensen不等式取等的情况猜想

由于，所以，为一次函数，以下略．

例2-38 证明：从任意三个不等的正数中，总能选出两个数，使得．

分析：这是一道竞赛题，也许刚开始一点思路都没有，但看到这个式子似乎联想到了高中学过的差角的正切公式，从而可设，

其中，从而问题转化为：在区间的任意三个角，总有两个满足，要说明正切值小于1，需存在两个角的角度的差要小于，为此，

将，由于，一定有两个角度要么属于，要么属于，

不妨设，且，则命题得证．

可见，对学过的数学公式，不只是知道套用，变形用，而是要把握其结构特征，从左往右能实现的功能，从右往左实现的功能等的进一步认识，这是学习公式的目的．

例2-38（2010清华大学自主招生）

已知函数是定义在上的奇函数，且当时，单调递增，．设，集合，

，求．

分析：由已知条件可画出函数的草图，如下：，

由草图可知，

，或时．

则集合是所有满足恒成立的的集合，即

，

所以，

在中，令，则等价于

对任意的恒成立，分离参数，，令，

问题转化为求在区间上的最大值，

在这里，可以求导，也可以用基本不等式，这里用后者推理如下：

，

当且仅当，即时取得最大值．

所以恒成立．

反思解决过程，有两个关键点：一是由已知条件画出函数图像的草图；二是对集合M、N含义及其关系的理解，所以，数学解题审题过程，对每一个条件数学含义的理解，理解得越深，越容易找到解决问题的思路．

例2-39（2011北京大学自主招生）

求函数的最小值．

分析：这是一道含有多个绝对值的一次函数构成函数的最值问题，和熟悉的或解决过的类似问题对比，最大的不同是“x”的系数不是1，所以，利用绝对值的几何意义的方法很难完成，那么，只能进行转化，也就是去掉绝对值，接下来怎么去想，如何求最小值呢？我们先回顾以下我们解决过的最简单的类似问题．

，画出图像，利用单调性，获得最小值；

，画出图像，利用单调性，求最小值；

，图像，单调性，最小值

若，不妨设，

当为奇数时，时，有最小值；

当为偶数时，时，有最小值；

所以，此类含绝对值的一次函数，本质上是分段函数，图象为折线段，然后从单调性入手，求得最小值．

设在时取得最小值，则

当时，即，时，

减函数．

，

，

①

当时，增函数．

②

联立①②，由于，所以．

例2-40 （2013全国数学联赛黑龙江预赛第22题）

设．

（Ⅰ）判断函数的单调性；

（Ⅱ）是否存在实数，使得关于x的不等式在上恒成立？若存在求出的范围，若不存在，试说明理由．

（Ⅲ）求证：

分析：（Ⅰ）第一问是常规问题，与高考的难度差不多，

，

由于（这是对数函数与其在点处的切线构建的基本不等式），

所以，得，

所以，函数在上单调递减．

（这样就不用二次求导了）

也可以构造新函数，，

所以在递减，，所以，在递减．

（Ⅱ）令，

，由于，所以，

①时，，递增，由于，得；

②时，，递减，恒成立；

③时，在递增，，不恒成立．

综上，．

（Ⅲ）由于时，恒成立，即恒成立，所以，即，，，令，即得结论．

例2-41（2015吉林预赛第15题）

已知不等式对任意的均成立，求实数a的范围．

令（）

若，则，则在递增，所以

若，则在上递减，在递增，

由于，而，所以，原不等式不恒成立．

综上，．

例2-42（2015湖南预赛第16题）

已知，，．

（Ⅰ）经过原点分别作曲线和的切线和，

已知两切线的斜率互为倒数，求证：；

（Ⅱ）设，当时，恒成立，试求实数a的范围．

（Ⅰ）设与曲线切于点，则

，且，即

解得，则，

由已知，即，

设（）

则，

当时，，时，

所以函数在上递减，在上递增

由于，，

所以函数在区间一定有一个零点

又，

所以

（Ⅱ），

，

由于，所以，

当时，，在递增，而，满足题意．

当时，由于，当时，，，

所以．

在递增，，

当时，（或者取，），

所以，在存在，

在递减，在递增，

所以，不恒成立，

综上．

例2-43（2012第八届中国北方奥林匹克邀请赛第6题）

设n为正整数，证明：．

分析1： 这是一个与自然数n有关的命题，自然想到数学归纳法，但用数学归纳法证明时的一个难点是要证不等式的右变是一个与n无关的常数，这样，由推时，右变必大于2，因此，需要根据验证步，获得一个比要证明命题更强的一个命题，也就是说比2小，且含有变量n，由，，……，猜想，再用数学归纳法加以证明，以下略．

分析2：根据所证式子的结构特征，可以直接构建函数，利用函数性质加以解决．

由于，分别令，

可得，

，

分析3：两边取对数以后构建函数．

，

构建函数，由于，

所以 ，

即，

而，证毕．

例2-44（2011清华自主招生）

已知函数，，，令，．

（Ⅰ）求数列的通项公式；

（Ⅱ）证明．

分析：这是一道函数、数列、不等式综合问题，第一问的思路比较常规，可以通过写几项，猜通项，数学归纳法证明的方法；也可以直接利用递推关系求通项，第二问通项求出来后，根据通项，对所证不等式进行等价变形是关键．

由已知求得，所以，．

方法1：观察、归纳、猜想、数学归纳法证明，略；

方法2：由于，考虑到式子右变是分子分母同为一次的分式形式，两边同时取倒数，得，即，这时数列部分熟悉的结构的形式，可以用待定系数法求出相应的系数．

，解得．

第二问在证明时，根据的结构特点，分子分母同为“一次”，

且分子为单项式，所以，所证式变为

，

即，

利用不等式

．

例2-45 乒乓球比赛，五局三胜制．任一局甲胜的概率是，甲赢得比赛的概率是，求为多少时，取得最大值．

分析：这道题看似一道概率问题，但本质还是函数最值问题．所以这道题的关键是将表示为的函数．

甲赢得比赛包括分三种情况：（1）若取胜，则概率是；（2）若取胜，则概率是，（3）若取胜，则概率是．

所以，

，

设，

是关于的五次多项式函数，直接求导，

，

当时，；

当时，；

所以，当时，取得最大值．

例2-46（2016北京大学生命科学冬令营）

设实数，且，则与的大小关系是

（A）> （B）=

（C）< （D）以上都有可能

分析：这道题要解决的问题是与的大小关系，也就说对做一个估值，而已知条件是之间的关系，所以，要进行两个方面的转化，一是将之间的关系系转化为之间的关系，二是将中的对数符号去掉，这时，我们自然想到，考虑到均为大于1的实数，可以利用，为此，

令，则

，

由于，

所以，．

例2-47 （2014清华自主招生）

已知，，求证：．

分析：这是一道不等式证明的问题，我们可以通过构造函数证明，同时，不等式中含有自然数n，可以结合特殊归纳完成；另一方面，根据所证式子的结构特点，也可以考虑整体解决．

思路1：设，

（），

（Ⅰ）时，，=1，成立；

（Ⅱ）时，令，

，

，

设（），

，

，

所以，命题成立．

思路2：即证

当时，显然成立；

当时，，

由伯努利不等式

．