适用经典的安全库存公式计算，有一个前提就是基于正态分布，毕竟这个公式的演化就是因此而来的。所以藉此计算安全库存，就是顾客的需求服从正态分布这个前提下进行。不过，如果不服从正态分布，经典安全库存公式的适用基础不存在，计算出来的结果就值得商榷了。

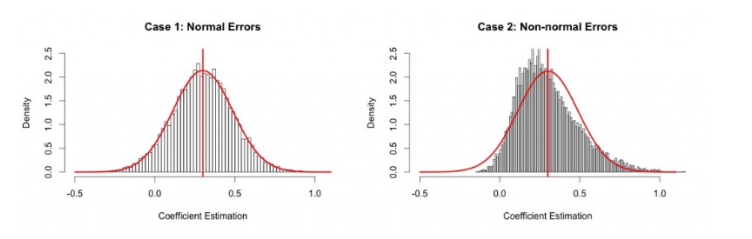
图3-21 正态分布（左图）和非正态分布（右图）的示例，来源于网络

在非正态的情况下，通过引入切比雪夫不等式用以考虑建立库存的量，以及可能缺货的概率。

19世纪俄国数学家切比雪夫（Chebyshev）在研究统计规律中，论证并用标准差表达了一个不等式。这个不等式显示了随机变量的几乎所有值都会接近平均。

其意义在于表示了

与平均相差2个标准差以上的值，数目不多于1/4

与平均相差3个标准差以上的值，数目不多于1/9

与平均相差4个标准差以上的值，数目不多于1/16

……

与平均相差k个标准差以上的值，数目不多于1/

其公式表示为

其中是随机变量，期望值为，标准差为。对于任何实数k>0。

和正态分布的覆盖95%的置信区间，只需要2个标准差所不同，切比雪夫不等式表示，非正态分布下，2个标准差只能覆盖75%。

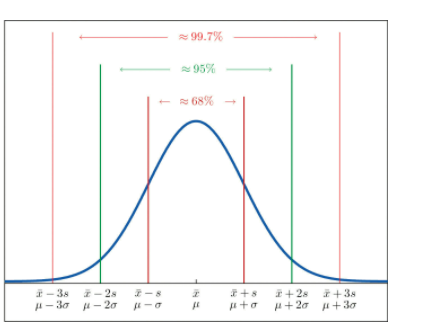
图3-22 标准正态分布图，来源于网络

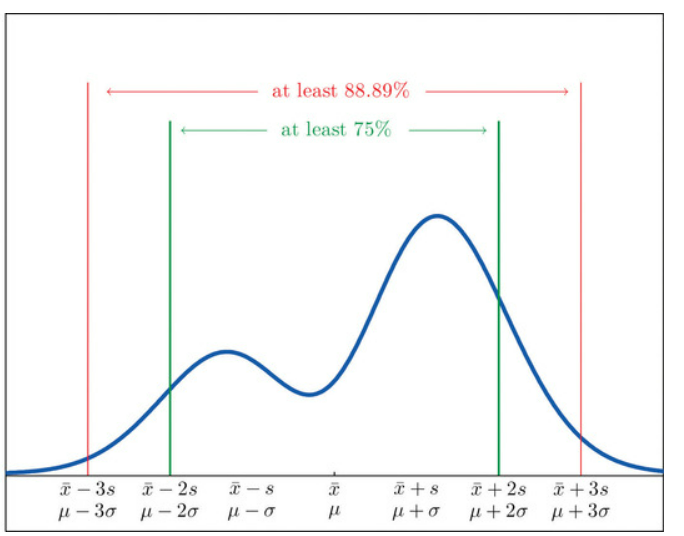
图3-23 切比雪夫不等式图例，来源于网络

切比雪夫不等式最大的特点就是适用任何分布形状的数据。这意味着在不确定数据是否服从正态分布的情况下，无法使用经典安全库存公式等来帮助建立库存策略的情况下，可以通过切比雪夫不等式，达到类似的效果。

不过这个不等式算出来的概率只是一个理论的上下界，仅仅是粗略地估计随机事件发生地概率，不甚精确。

某公司过去12个的销售数据如下，虽然并没有验证分析，不过存在很大的可能性是该数据分布并不服从正态，并通过这个12个数据得出了月均销售和其标准差。

表3-26

当下一个月预测的销售数据为60000个单位的时候，并且当前并没有任何库存在手或在途，随之订货60000个单位来满足未来需求。那么通过切比雪夫不等式来估算出大概有多少概率可以满足需求而不会缺货。

订货60000个单位，也就是期望值为60000，平均值是35866，标准差是31554，套入不等式公式的一边，即I 60000-35866 I >= K * 31554，得出K值最大为 0.76 然后么再套入不等式另外一面，即约束条件1/，得到1/ =0.5776 ，意味着60000的订货量，根据过往情况来看，将近57.76%的概率不会缺货。

尽管这是一个估算的概率，不过当对数据真正来源知之甚少，并不能确认它服从什么类型的分布，那么作为一个分析随意类型数据分布的工具来说，切比雪夫不等式有着很重要的指导作用。通过其计算，对于如何应对未来需求这个不确定的随机因素，并因此建立多少的库存量，它的结果能够带来相对的范围概念。

切比雪夫不等式求的结果，只是对概率的一个估计，是一个提供一定理论数字支撑的工具。在现实中，必须要考虑到更多涉及供应和需求的因素，来衡量建立库存的合理性。比如说，在此基础上有未来三个月的销售预测如图3-24折线表示

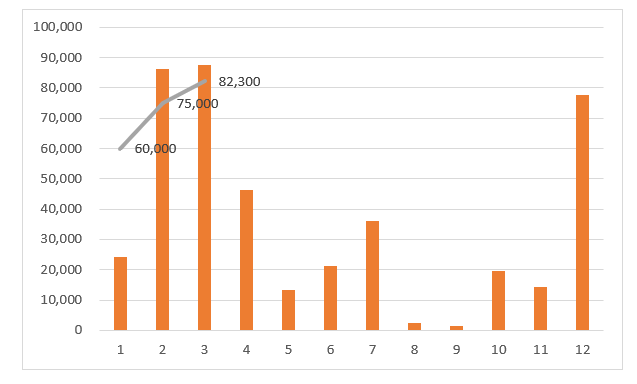
图3-24

这样的情况下，未来的销售预期比以往要很，而且呈现良好的上涨趋势，那么以过往历史实际作为概率计算基本数据就有一定的风险性，所以可以考虑再适当加大一点库存量，从而减少缺货的概率。