一元线性回归模型假设被预测变量 y和单个预测变量 x之间存在线性关系,其公式可以表示为
系数 a和 b 分别表示回归线的截距和斜率。截距项 a表示当 x=0时 y 的预测值;斜率 b 表示当 x 增加一个单位时,y 的平均变化。这种寻找一条通过数据集的最佳直线,就是回归分析。它有助于在不同分布的数据中,找出穿过数据的直线,并使得每一个数据点到这条直线的距离平方和达到最小。
一元线性回归的一元指的是只有一个自变量(即外部因素),从而带动因变量(在预测中指需求量)变化。
某公司自第1周开始上架某SKU,每周推出一定的折扣优惠,随着折扣的力度越来越大,销量也因此增加。
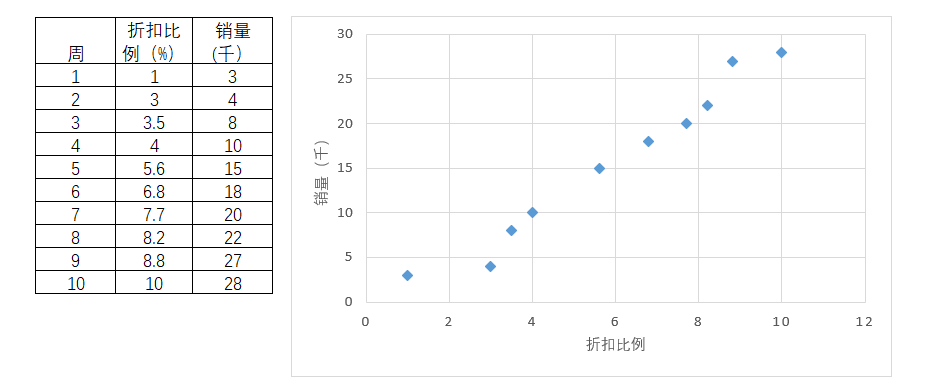
图4-29
当这个折扣比例被认为是影响销量的因素时,并根据情况(图例)发现随着折扣力度越大,销量也因此因相应地增加,那么可以认为这两者之间存在关联。对此试图建立回归直线来进行分析。
利用Excel,选择数据-数据分析-回归,进行相应的选择。其中Y值输入区域表示为因变量,X值得输入区域表示为自变量,按下确定就可以得到相关回归方程所需要的数据了。
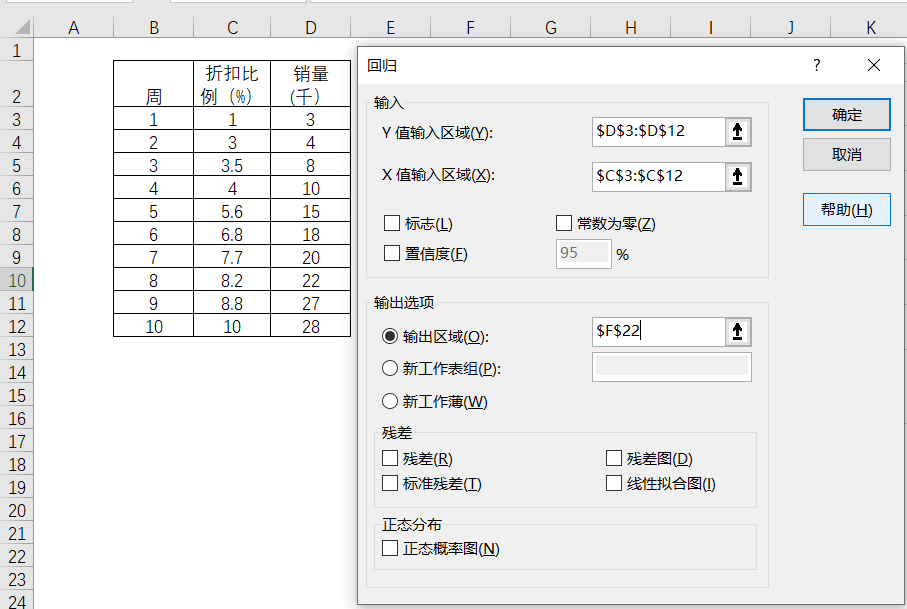
图4-30
得出的结果如下:
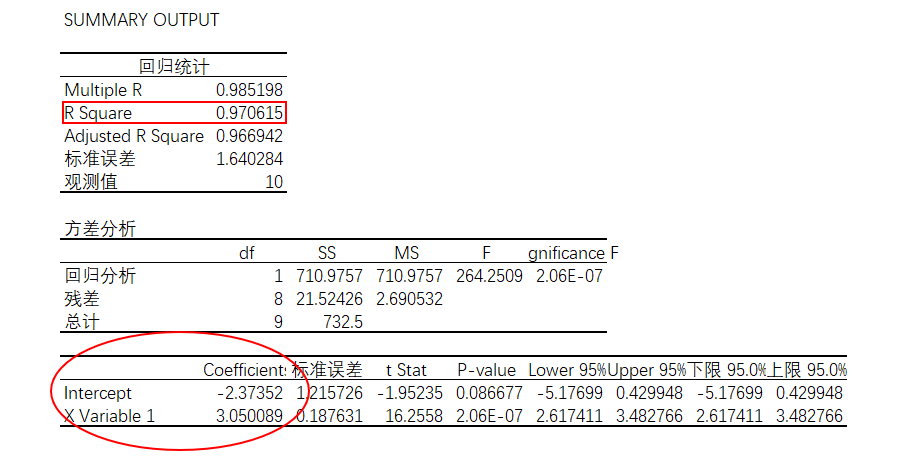
图4-31
根据图4-45得出的结果,可以建立线性回归方程,即,如下图,而各点与直线之间的距离,表明实际和预测之间的差异,也通说说明了除了X这个因素之外,还有其他的因素导致实际值和预测值有所不同。
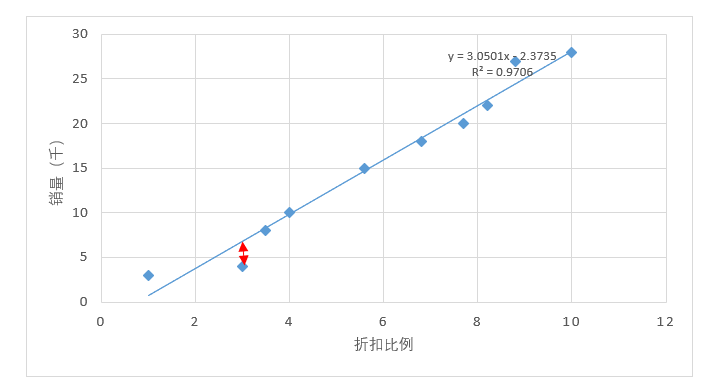
图4-32 线性回归方程图
根据建立的回归方程,如果下一周继续同样状况并继续加大折扣力度,折扣比例为10.5%,预测得出的销售量为30(千)(数据四舍五入)
根据这个一元线性回归方程而建立的预测法究竟是否合适呢?当然通过看图,感觉是合适的,将折扣比例作为自变量,而将销售实际作为因变量进行线性回归分析,能通过看出折扣比例对销售实际产生了影响关系。
还可以通过R平方值(图示中的R Square)来观察,如计算结果,R平方值等于0.9706,意味着折扣比例可以解释销售实际的接近97.06%变化原因。当这个值等于0时,表明自变量和因变量没有任何的关联,而当这个值等于1的时候,表明两个变量之间具有完美的不具有任何干扰的线性关系。
一般来说,>0.7是高度线性相关,0.3和0.7之间是中度线性相关,<0.3是低度线性相关。当R值(R平方值的平方根,也叫相关系数)为负值,则说明自变量和因变量是负相关,可以理解为发展趋势呈向下发展。本例中R值为0.9851,表明是高度的正相关。如果是R值偏低,暗示了还有其他更为重要的影响因素存在。
R平方值容易偏大估测回归模型的解释能力,随着自变量数量不断增加,R平方值也会增加,让回归模型拟合的效果更加好,但是实际情况并非如此,因为可能存在某些自变量和因变量并不相关,增加这些自变量不会有助于拟合度的增加。因此,调整的R平方值就是用以解决这种可能过于乐观的情况,并更能代表销售实际值中能被解释的部分。本例中调整的R平方值为0.9669。
因此,本例中的R值,R平方值和调整的R平方值,表明折扣比例和销量,存在很强的正相关线性关系,并且这种绝大部分这种变量关系是可以解释的。
【小插曲1】置信度和置信区间到底是什么
在Excel的回归计算中,选择中有一个关于置信度的项目,见图4-65,默认值为95%。这个选项除了在Excel中,在不少的软件计算中也同样存在,多数的默认值也是95%。
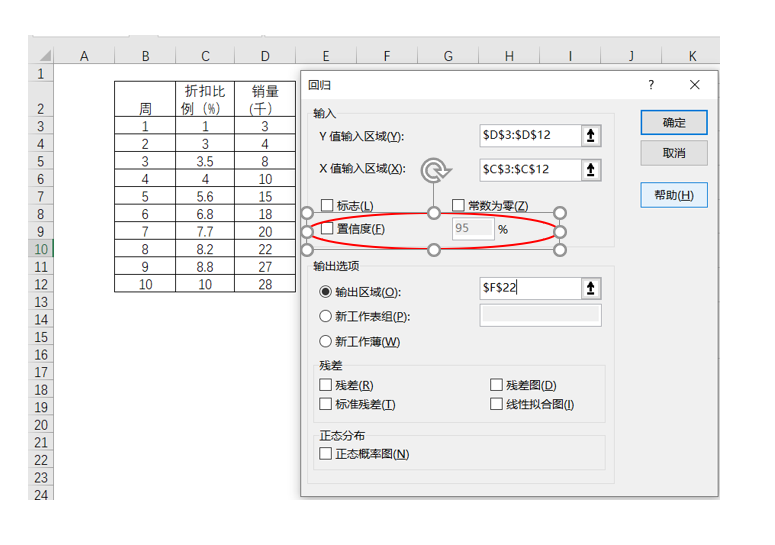
图4-33
进行预测运算的过程,实际是在寻找随机变量的过程中,找出可能取值范围内的中间值。通常情况下,预测会伴随着一个预测区间,给出一个随机变量具有较高概率的范围值。这个区间反映的是,估算究竟准不准,准的话,那么准确度又有多大呢?
比如小李最近的三次高考模拟考试得分是620,625,615分,那么预测他高考成绩是620分。这个值称为点估计,只是这个是一个非常确切和精准的数值,而高考过程中涉及了很多因素,小李有可能得到这个成绩,当然也可能不是这个分数,那么这个预测的估计值就不是非常可靠,为此要人更加信服的话,就设立一个区间,以这个620分作为平均值,并让这个区间作为上下限,其上下限的值就是该平均值加上或者减去某个标准误差。根据过往模拟考试的成绩,小李取得的分数非常可能是在615分到625分之间,而这个非常可能换算成数字的话,就是有95%的把握。这个95%就是置信度。而615分和625分就是置信区间的上下限了,记为[615,625]。
置信度和置信区间一般是相同趋势。当置信度很高时,置信区间也会很大;当置信区间很大时,置信度也会很高。如果高考满分是750分,置信度是100%,也就是小李的高考分数必然能够预测中,那么分数的置信区间,就是从0分下限直到750分上限这个跨度了。
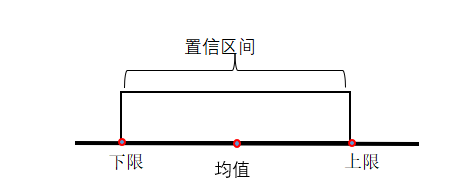
图4-34 置信区间
置信区间的上下限计算公式为
这里涉及了Z值的计算,对于Z值,在库存里谈到过了Z值和对应的概率的。
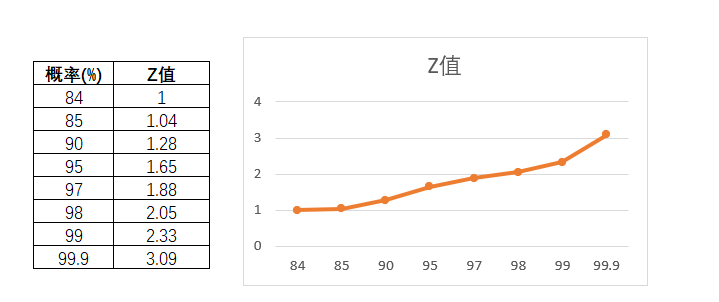
图4-35
而90%的置信度,对应的Z值是1.65(见图4-67),可是对应的概率却是95%。对于这点,常常让人混乱。为什么查找置信度是90%的Z值时,要查找95%对应的值,或者在Excel中输入Nrom.d.inv函数时,输入的是norm.d.inv(0.95)而不是norm.d.inv(0.9)呢?
通过图示可以容易理解,90%的置信水平就是上限和下限内的包含90%的面积,而除外还有10%的面积,各自平均分一半在两侧,即每侧5%。而95%的概率就是0%开始直到置信区间的上限值。因此90%的置信水平,对应的是95%的概率,也就是说,Z值是取值95%的概率对应值。
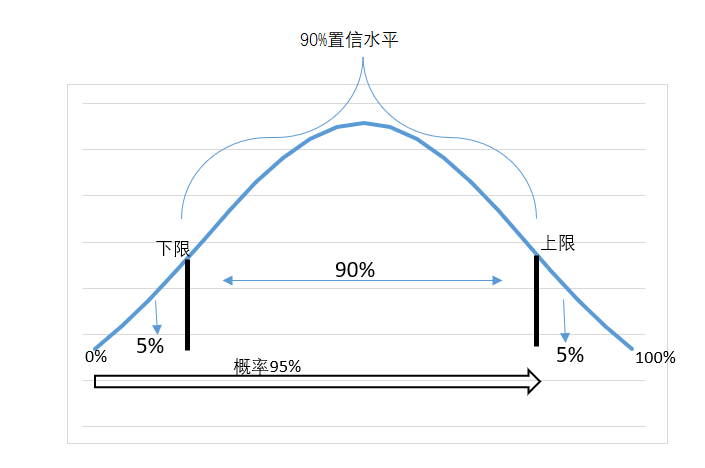
图4-36
【小插曲2】线性回归预测遇见季节性因素,怎么办
某品牌的运动鞋在2017年到2020年的各季度销量如表4-44所示。
表4-44
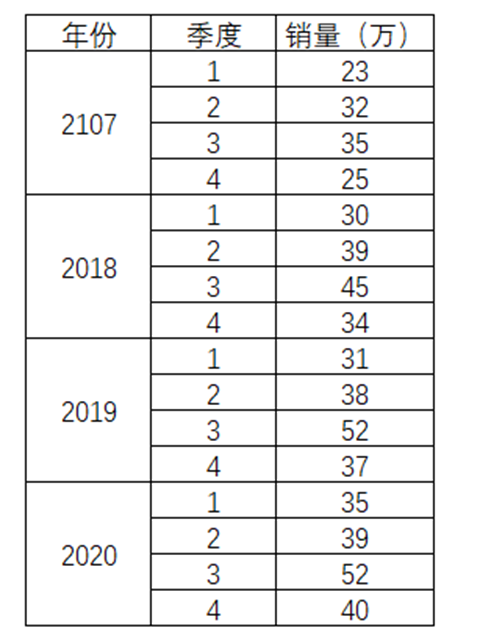
并且通过图示观察,呈现出线性趋势的情况。
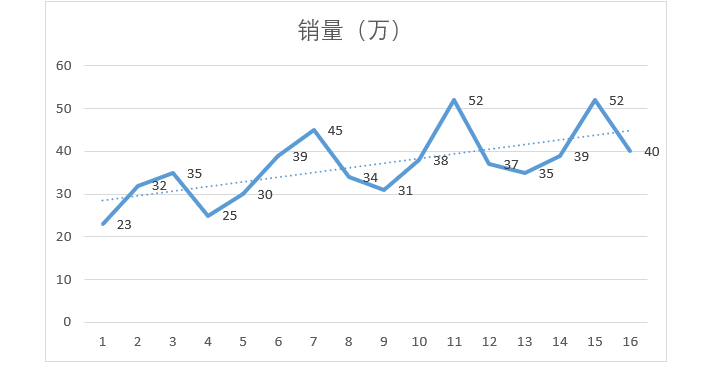
图4-37
然后拆解出各个年份对比,图形都是很雷同,都是从第1季度开始增长,在第3季度达到顶峰,然后在第四季度回落。
表4-45
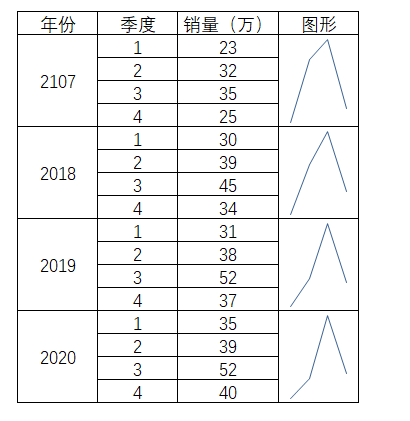
综合以上,这个历史数据表示趋势具备了线性和含有季节性因素。
该品牌打算利用以上数据,使用时间序列法的预测,就要把线性回归和季节性模型结合起来。线性回归,如果是一元线性回归,就是,如果是涉及多元,就要再增加自变量。历史数据表明含有4个季节性的因素,那么可以把每一个季节看作一个自变量因素。
但这里涉及一个哑变量的问题。因为要把季节因素融入到线性方程中,就是需要做哑变量处理。季节因素被视为分类变量,而所谓分类变量就是用于将数据观察值分类的数据。
假如没有处理,直接代入,把第一季度看成是X=1,第二季度看成是X=2,如此类推,那么线性方程是Y= A + BX,而回归系数B描述了自变量X每增加一个单位对因变量Y 的影响,不过把季节视为一个自变量因素的话,然而当季节从1变化到2,又或者从2变化到3,它对因变量Y的影响应该是不尽相同的,如果按照线性方程Y= A + BX而言,这个影响都是一样的话,这样的话实际还是单纯的线性回顾,并非融合了季节因素。
所以,对于这样的分类变量,就是进行哑变量处理。
对四个季度,启用了3个虚拟变量,分别命名为Q1,Q2,Q3,其值只能为0或1。当表示为第一季度的时候,Q1为1, Q2和Q3都为0;表示为第二季度的时候,Q2为1,Q1和Q3都为0;当表示为第三季度的时候,Q3为1,Q1和Q2都为0。那么3个虚拟变量就可以决定4个分类变量,也就是第四季度的时候,Q1,Q2和Q3都为0。
表4-46
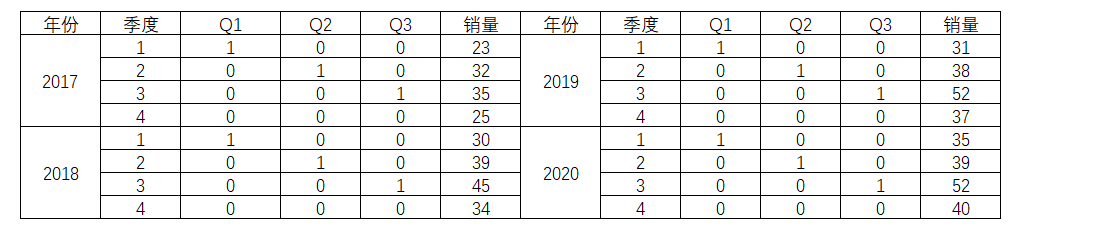
这样的话,回归方程就变成
Y=A+BX1+CX2+DX3+Et
这个公式含有三部分要素,第一项是截距,最后一项是时间线性趋势,中间的都是季节性影响,其中t是时间周期。
那么就可以理解为,当X1从0变化到1,X2和X3均保持不变,那么变量就从第1季度变化为第4季度了。
首先把相关数据整理入EXCEL,并根据上述的方程式建立预测值的计算,其中相关参数A到E可以先行随便设置。再把相关数据整理入EXCEL,并根据上述的方程式建立预测值的计算,其中相关参数A到E可以先行随便设置。
表4-47
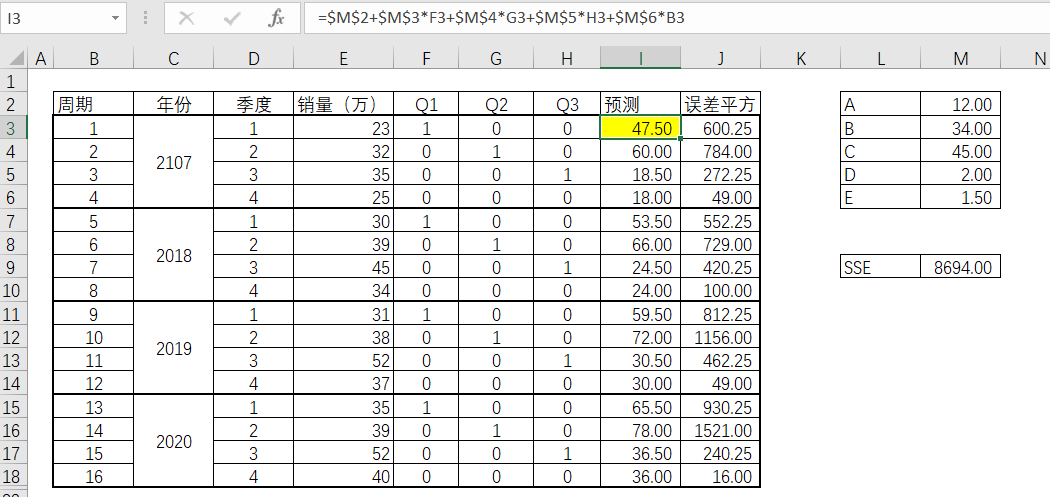
第一步动作,就是通过预测和实际值的最小误差平方和(SSE),来求出对应的A到E值。
利用EXCEL的规划求解。注意:A到E的参数并非一定要正值的,所以“使无约束变量为非负数“不要打勾选择。
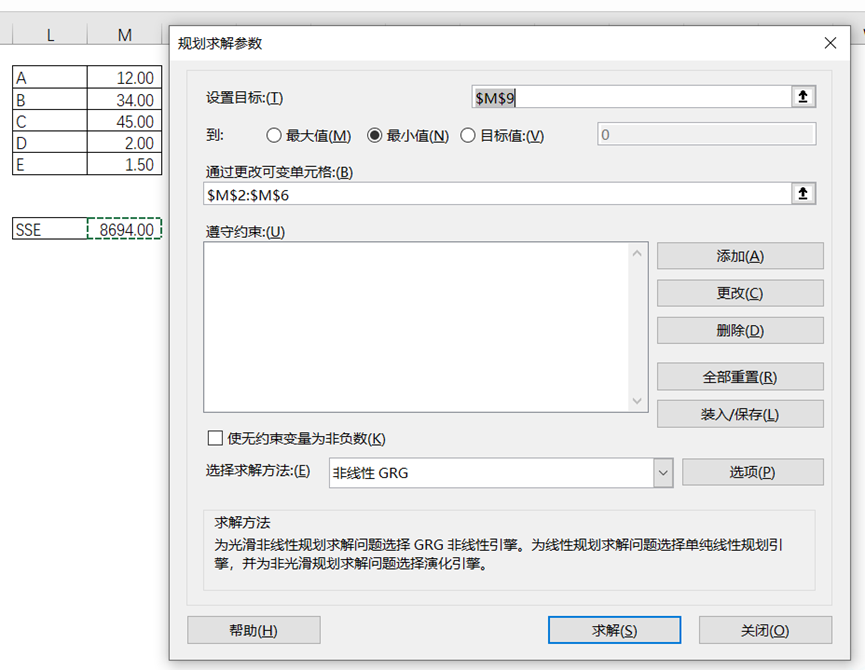
图4-38
预算后的得出结果如图表4-48。
表4-48
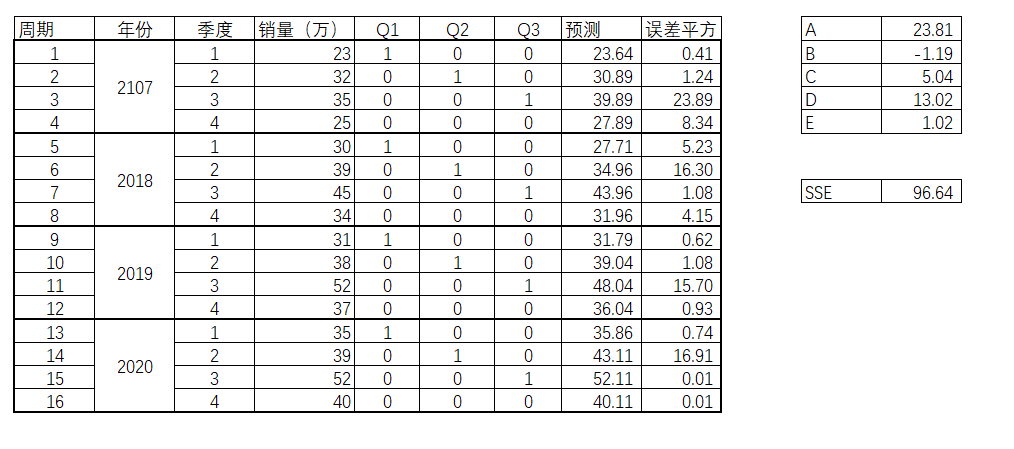
就意味着公式Y=A+BX1+CX2+DX3+Et代入A到E各参数后变为如下:
Y = 23.81-1.19X1+5.04X2+13.02X3+1.02t
斜率是1.02,意味着每一季度大概增长1.02万的销售量。那么,下一年(2021年)的4个季度的预测值也因此得出, 如表4-49。
表4-49
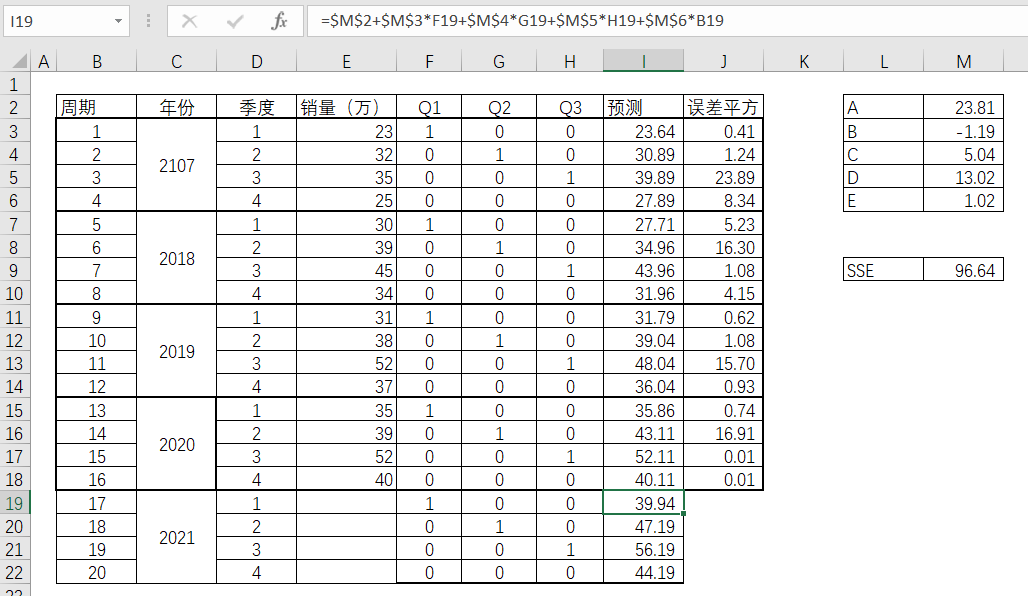
通过图4-39来看,拟合度还是不错的。
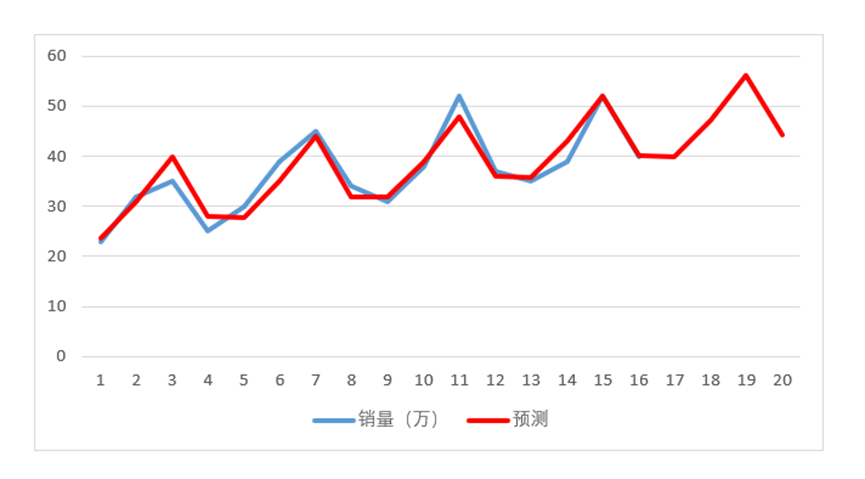
图4-39
该品牌为了进一步验证,通过Excel的数据分析来对比。根据Excel中的数据分析-回归,查看拟合度情况如何。
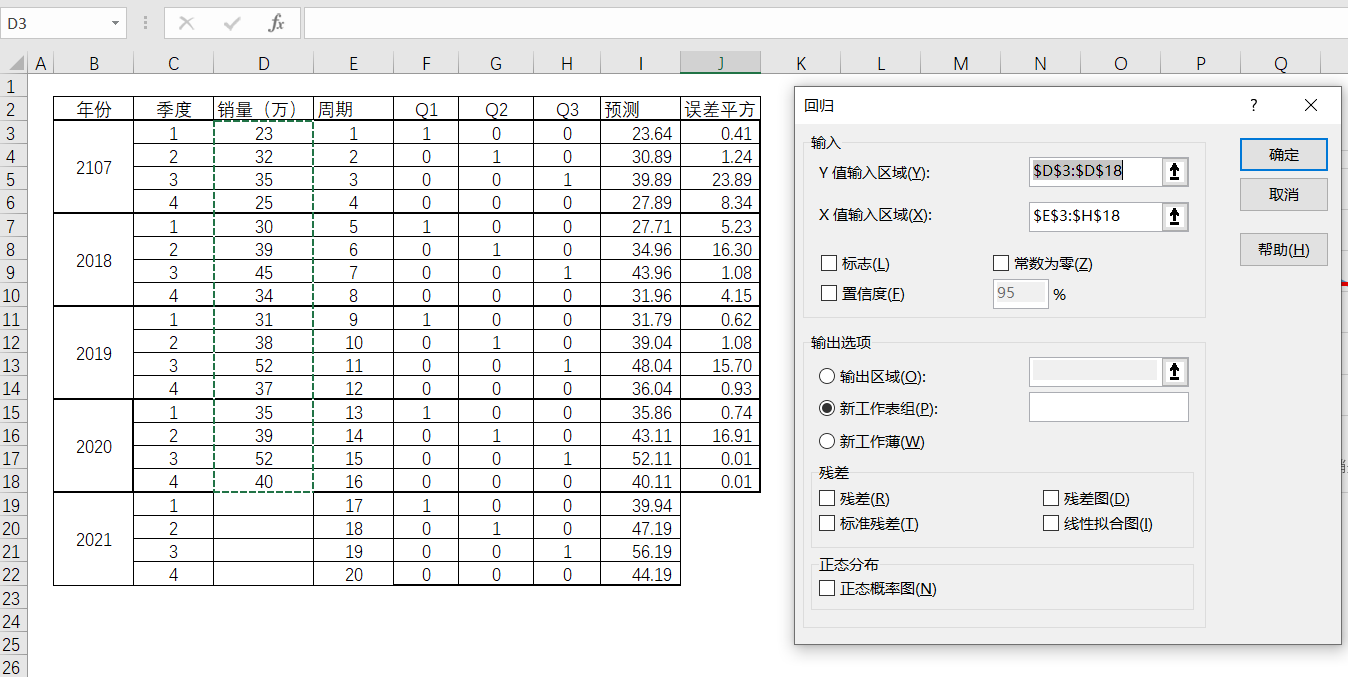
图4-40
Excel得出结果如图4-41,R方和调整后的R方还是不错的。因此该品牌考虑采用相关的预测值。预测数值并非最终绝对,该品牌还要结合市场因素等做出调整。
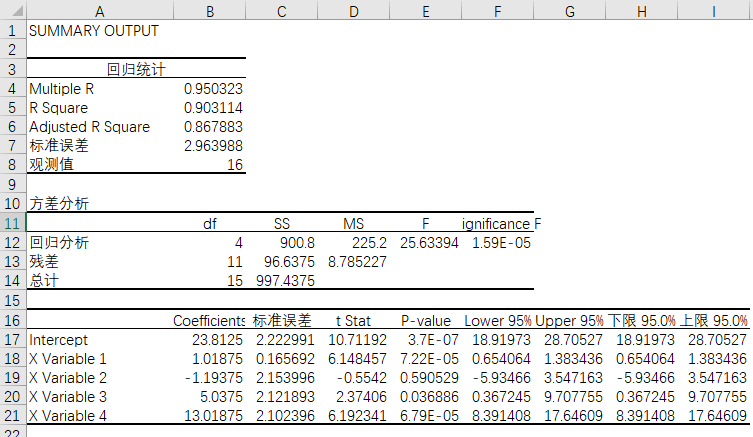
图4-41


 不详
不详

