学习曲线将学习效果画在坐标图上，横轴表示学习次数，纵轴表示学习效果。在生产实践中，学习次数通常用累计产品产量来表示，学习效果用累计平均工时表示，因此，学习曲线表示了产品制造工时与累计产量之间的变化规律。

表1-10 工时累计表

图1-15 学习曲线

图1-15中是某飞机厂的飞机构架加工制造的学习曲线。表1-10中所列的就是和图1-15对应的相关数据。表中第1列表示产品的累计产量数，第2列表示与这个累计台数相应的单台产品直接人工工时。由于表中取得累计产量的关系都是增加一倍（翻一番），即累计产量为2n。这样单台（件）产品直接人工工时按20%递减的规律就清楚地显示出来。

就是说加工制造第2架飞机构架的工时只有第1 架的80%，加工制造第4架飞机构架的工时只有第2架的80%，第8架只用了第4架工时的80%，第16架只用了第8架工时的80%等。

第3列为累计直接人工工时，将第3列累计直接人工工时除以第1列产品累计数，就得到第4列的累计平均直接人工工时。

从图中可知，随着累计产品产量的增加，产品累计平均工时在递减，但其递减速度却随累计产量增加而逐渐变小，直到趋于稳定。

为了利用学习曲线进行定量化分析，需要将它表达为数学解析式。按上述学习曲线现象所反映的规律，它的变化呈指数函数关系，可用以下关系式来表示：

式中，Y为生产第X台（件）产品的工时；K为生产第1台（件）产品的工时；C为工时递减率或学习 率；X为累计生产的台（件）数；n为累计产量翻 番指数。

对上面两式取对数，可得：lgY = lgK + nlgC

lgX=nlg2

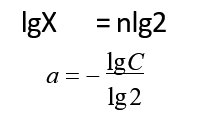
设式中，a称为学习系数。由此可得：

lgY= lgK-algX

从而得出Y=KX

它表示了学习效果即累计平均工时Y随累计产量X（即学习次数）而变化的情况。

利用莱特公式，能更为精确地得到计算结果。例如，要想求得生产第32台飞机构架时的直接人工工时，则将已知数值K=100000，C=0.80，X=32代入即得

Y32=100000×32-a

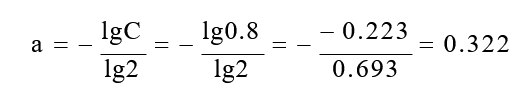
得出

在莱特公式Y=KX 中，由于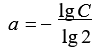，所以当学习率为一定时，学习系数也是一个定值，如表1-11所示。

表1-11为学习率与学习系数对照表

表1-11 学习率与学习系数对照表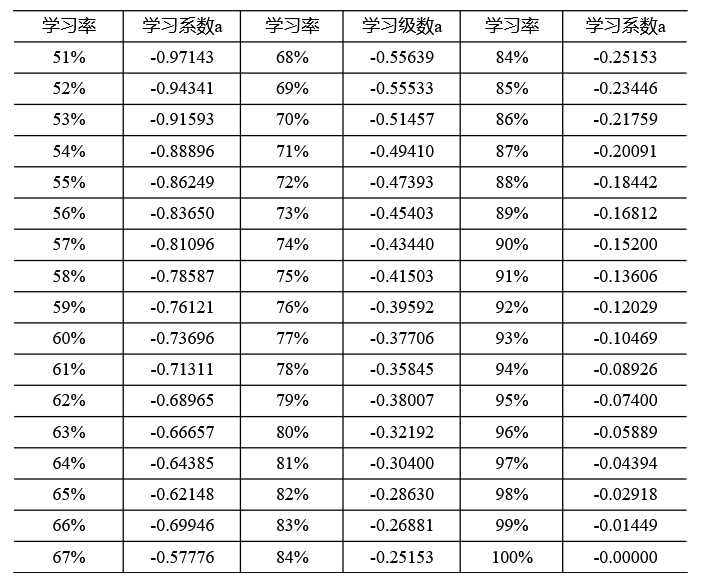

由莱特公式可知，要想求生产第X台（件）产品所需工时，必须已知学习系数a，然而a与学习率C存在一定的关系，即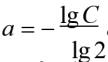。因此若能确定学习率C，就可求得学习系数a。确定学习率方法常有直接测定法、历史资料法、经验估计法、合成法、MTM法（方法时间测定）。

这里介绍直接测定法如下：

由莱特公式可知，K为生产第1件产品的工时，可通过实际观测得到，a为学习系数，是一个参数。如果对生产情况进行现场观测，求得参数a的估计值，再根据 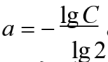，从而求得学习率C。

例：已知某机械厂生产某种机器，第10台的成本为3000元，生产第30台的成本为2000元，求该产品的学习率。

解：由已知条件可得：

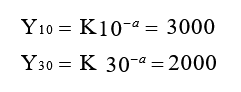
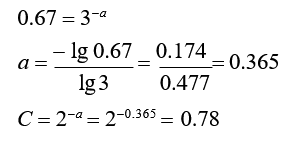
故该产品的学习率为78％。

国外专家学者研究表明，学习率的范围在50%～100%之间。当人工作业时间与机器加工时间比例为1:1时，学习率约为85%；当人工作业时间与机器加工时间比例为3:1时，学习率约为80%；当人工作业时间与机器加工时间比例为1:3时，学习率约为90%；当机器完全处于高度自动化状态加工零件时，无需人工作业配合，则学习率为100%，它意味着加工一批零件的第1件产品与加工最后1件产品的工时相同。

由此可见，人工作业时间所占比例越大，学习率就越低，学习系数就越大，反之则学习率越高，学习系数就越小。工程实际应用中，通常学习率大约在75%～95%之间变动。