（一）已知曲线求方程

一般情况下，平面直角坐标系下的曲线或区域都可以通过其上一点的横纵坐标x，y满足的等式或不等式组加以表示．由于曲线可以看作是满足某些条件的点的集合，这些条件，就是动点在运动过程中的（几何）不变性，将这些不变性用其对应点的坐标x，y表示出来，即可得到曲线的方程：．在具体解决动点轨迹问题的过程中，可分为两类：

1.若所求轨迹问题根据可以圆锥曲线的定义（第一或第二定义）判定其曲线类型，则可用待定系数法求其方程．

例1 过定点M(4,2)任作互相垂直的两条直线和，分别与x，y轴交于A、B两点，求线段AB中点P的轨迹方程．

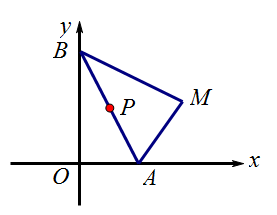
【分析1】如果事先不能利用几何关系获得动点满足的几何性质，求点P的轨迹方程时，可设，接下来，只要求出点P的横纵坐标x，y应满足的关系式即可．那么，如何才能建立x，y之间的关系呢？利用点P在运动过程中的不变性（几何性质），即点P是线段A、B的中点，而A，B分别是过点M的两条互相垂直的直线和与x，y轴的交点，所以，可以通过过点M的直线的斜率k作为参数建立x，y之间的关系．由题意，存在且，可设，则．

对于，令，得；

对于，令，得．

则

消去，得，

所以，方程即为点P的轨迹方程．

【分析2】由于解析几何研究的对象终究是几何问题，所以，我们没有必要一味的用代数方法与代数运算去解决问题，有时候，从分析几何图形所具有的几何性质出发，可能使得运算过程大为简化，这是解决解析几何问题的重要策略．对于本题而言，由于直角三角形和的斜边为，所以，四点共圆，其中P为圆心，进而，，即点P的轨迹为线段OM的垂直平分线，所以，动点的轨迹为线段OM的垂直平分线，其方程为，即．

例2 满足条件AB=2，的三角形ABC面积的最大值是 .

【分析1】此问题可以较容易地从解三角形和函数的角度寻求解题途径，这可以看作是解决此问题的通法．

设，则，为了求面积，引入参数，则

，利用与的关系，将面积转化为关于的函数，

，

而，

，

，当时取等号．

从上述解题过程可以看出，这种方法对函数思想和运算求解能力要求很高，而且，作为填空题，即使能做对，由于用时较长，容易造成潜在失分．

【分析2】用坐标法，将几何问题坐标化．建立适当的坐标系，

设，，则

，，

，．

C点在圆心是，半径为为半径的圆上，AB在圆的直径上．

（当然，也可以直接利用圆的第二定义：在平面上给定两点A、B，设点P在同一平面上且，则点P的轨迹为圆）获得圆的方程．

所以，，当且仅当取得最大值．

例3 设圆的圆心为A，直线l过点且与x轴不重合，l交圆A于C、D两点，过B作AC的平行线交AD于E，求E点的轨迹方程．

【分析1】 定义法

由题意，三角形ACD是等腰三角形，

又，即，

所以，

又，所以，三角形EBD为等腰三角形，即，

，所以，点E的轨迹为以焦点，长轴长为4的椭圆，其方程为（）．

分析2 交轨法（如果事先没有判断出曲线的类型，可用此法．）

设直线AC的方程为，

联立方程组，整理得

，由于，

设，则，．

直线AD：，直线BE：，

联立方程组，将代入

……①，……②

①+②，得；①×②，得

消去，得，由题意．

所以，点E的轨迹为以焦点，长轴长为4的椭圆，其方程为（）．

2.若无法判断曲线类型，则一定要关注动点运动变化的过程，寻找出动点变化的主要因素，恰当设参，将动点满足的几何不变性坐标化，进而消参求出方程．

例4 已知椭圆，直线．P是l上一点，射线OP交椭圆于点R，又点Q在OP上，且满足．当点P在l上移动时，求点Q的轨迹方程．

【分析1】：由于此题很难通过所给几何条件判断动点的轨迹类型，所以要用交轨法．由题设可知，点Q不在原点．设P、R、Q的坐标分别为(xP，yP)，(xR，yR)，(x，y)，其中x，y不同时为零．

当点P不在y轴上时，由于点R在椭圆上及点O、Q、R共线，得方程组

，由此可解得

由于点P在直线l上及点O、Q、P共线，得方程组

，

解得

当点P在y轴上时，经验证①－④式也成立．

由题设|OQ|·|OP|=|OR|2，得

将①－④代入上式，化简整理得

因x与xp同号或y与yp同号，以及③、④知2x+3y>0，故点Q的轨迹方程为

(其中x，y不同时为零)．

所以点Q的轨迹是以(1，1)为中心，长、短半轴分别为和且长轴与x轴平行的椭圆、去掉坐标原点．

此方法可以看作是通法，思路容易想到，但引入的参数较多，消参时对代数运算的能力要求较高．

【分析2】（对【分析1】的改进）：

由于几何条件|OQ|·|OP|=|OR|2，化为的形式后，具有明显的几何意义，利用三角形相似的相关知识，可得到其坐标形式为，再利用【分析1】的结果可得，即，这样，运算量就减小很多了．

【分析3】：分析P点的运动过程，可以看作是由射线OP的旋转引起的，故而设直线OP的方程为，这里k为参数，

则P点的坐标可由方程组解得．

R点坐标由方程组解得．

再由|OQ|·|OP|=|OR|2，可得，即

，即，化简可得，所以P点的轨迹方程为(其中x，y不同时为零)．

练习

1. A、B是两个定点，，动点M到A的距离为4，线段MB的中垂线L交AM于P点，当M变化时，求P点的轨迹方程．

2. 双曲线，右支上一点M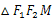，的内切圆与x轴切与P点，则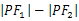的值等于

3. 已知动圆P过定点A（-3,0），并且在定圆B：的内部与之相切，求动圆圆心P的轨迹方程．

4. 已知点A（4,0），点B在曲线上运动，求线段AB的中点P的轨迹方程．

5. 已知每条棱长都为3的直平行六面体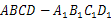中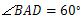，,长为2的线段MN的一个端点M在上运动，另一端点N在底面ABCD上运动，则MN中点P的轨迹与该平行六面体表面所围成的几何体中较小体积值为 ．

（二）根据曲线方程研究曲线的几何性质

有了曲线的方程，我们就能够对二元方程用代数方法进行研究，进而得到曲线的更进一步的几何性质．在用代数方法研究几何性质的过程中，恰当利用曲线的几何性质可以简化代数运算的繁简程度．

1.如何根据曲线C的方程研究曲线的几何性质

（1）研究曲线C的范围

由于在曲线方程中，变量之间存在制约关系，因此，我们可以利用函数观点，将二元方程变形为，或，或关于的二次方程，利用式子有意义获得的范围，同理也可获得的范围．

例如，要研究曲线方程的性质，首先可将其变形为，要使此式子有意义，必须，即．同理可得，此时．因此，曲线的范围是

在求曲线的范围时，可将方程化为，由于关于的方程有实数解，所以，解得，同理可得

．

（2）研究曲线C的对称性

对于曲线C的方程，若二元函数满足：

①，则曲线C关于轴对称；

②，则曲线C关于轴对称；

③，则曲线C关于原点成中心对称；

④，则曲线C关于直线对称；

⑤，则曲线C关于直线对称；

⑥，则曲线C关于直线（c为常数）对称；

（3）研究曲线C的顶点、与坐标轴的交点等

曲线C的顶点是指曲线与其对称轴的交点，例如曲线的顶点就是方程组

的解对应的点.

（4）曲线的离心率

可以根据各自曲线的类型求其离心率．

（5）曲线的切线

这里的曲线是指圆锥曲线．圆锥曲线的切线是指与圆锥曲线有且只有一个公共点，且圆锥曲线在直线的同一侧．求曲线的切线时，可以用待定系数法以及切线的定义，通过联立方程组求解．也可以将曲线在某一象限的部分看作函数图像，从而利用函数的求导加以求解．

例5曲线C是平面内与两个定点,的距离积为的点的轨迹．给出下列三个结论：①曲线C过坐标原点；②曲线C关于原点对称；③若点P在曲线上，则的面积不大于．其中，所有正确结论的序号是 ．

【分析】设曲线C上任一点，则，曲线C的方程为

．由于，时，方程不成立，所以，第一个结论显然不正确．第二个结论正确，因为若点在曲线上，则点也在曲线上．

第三个结论正确．设与的夹角为，则

．

例6 若直线与圆的位置关系是 ．

【分析1】由于直线方程与圆的方程已知，用代数方法，只需要求出圆心与直线的距离，再与圆的半径相比即可得出结论．

圆的标准方程为 ，所以，圆心，半径．

圆心到直线的距离，

由于，，

由于，所以，从而，．

直线与圆相交．

对于一道填空题而言，这样的解法有点“小题大做”，而且能力要求较高．实际上，在用代数方法研究几何问题的过程中，如果能够充分挖掘代数表达式中参数的几何意义，就可以使运算难度降到最低．

【分析2】由于所给直线方程中含有两个参数a和b，将所给方程

可化为，无论a和b取何值，直线恒过点，而点在圆内，所以直线与圆相交．

比较两种方法，我们对用代数方法研究几何问题有了新的认识．

例7 对于椭圆，若点满足，则称该点在椭圆内．在平面直角坐标系中，若点A在过点的任意椭圆内或椭圆上，则满足条件的点A构成的图形为

A.三角形及其内部 B.矩形及其内部 C.圆及其内部 D.椭圆及其内部

【分析1】这是一道新定义问题．由于“点A在过点的任意椭圆内或椭圆上”，若设，则，且点在椭圆上，即，问题转化为获得之间的关系 ，进而判断对应的图形．

下面我们消去参数a和b．

由，得，代入，得

即，进而

由，得，

令（也可以分离常数）

问题转化为对任意，恒成立，求之间的关系．

①时，只需，即，所以或．

②时，当时取得最大值，只需即可，所以

③时，无最大值，对任意不恒成立．

综上，点对应的区域为矩形及其内部．故选B．

当然，在具体操作过程中，也可利用两个参数直接判断，具体如下：

，且，

即，化简，得 ，

要使不等式对任意a，b成立，只需，从而得到问题的答案．

【分析2】：由椭圆的对称性知，经过点的椭圆，无论ab取何值，对应的椭圆必经过，，，且以上述四点为矩形都内接于椭圆．假设在四点矩形区域外有一点M，则一定存在一组使得点M在椭圆外，因此选答案B．

读者可体会上述思想，完成下面的问题：

练习：

1．已知，求的最值．

2．若直线通过点M（），则

A. B. C. D.

3．直线与圆相交于A，B两点(其中a，b是实数)，且三角形AOB是直角三角形，则点与点之间距离的最大值为 .