多元线性回归是从一元线性回归延伸而来的，也就是具备了两个或以上的自变量，并且都对因变量起着影响作用。其公式如下

某物流公司进行一个运输作业项目，它执行了10回作业任务，每次具体的运输里程，运输次数和运输时间都留有记录。

表4-50

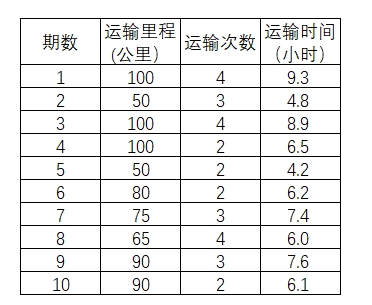
第11回作业估算要跑102公里，涉及6次运输次数，那么预测其所使用的时间，则可以考虑使用多元线性回归进行预测。因变量Y就是运输时间，是将要进行预测的项目，而自变量X就是运输次数和运输里程。根据这个通过Excel进行数据分析。

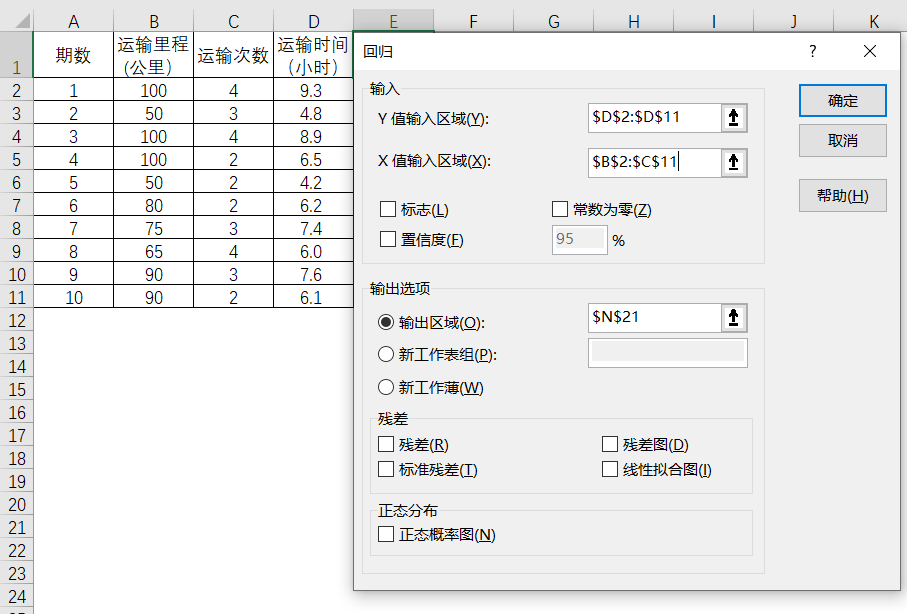
图4-42

得出的结果如下

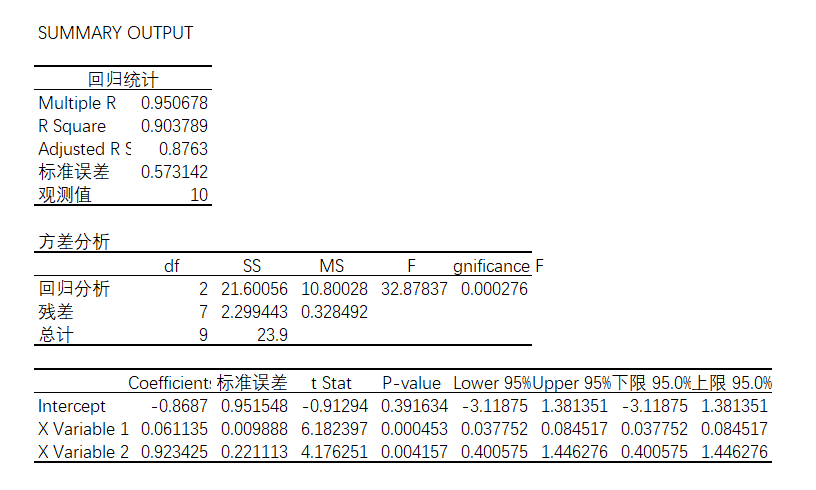
图4-43

则多元线性回归方程为

并且R值为0.95，具备很强的正相关性，而R平方值为0.903，意味着运输次数，运输里程可以解释运输时间的90.3%的变化原因，调整的R平方值为0.876。由此看来这个回归方程还是比较适合的。

当要计算第11次作业的运输时间，只需要代入相关数据到方程，就可以得出预测的运输时间为10.8小时。

【小插曲3】假设检验证明：认识T检验和P值

在上述例子中，进行回归的数据分析，得到多个t值和p值，在多元线性回归方程中，涉及多个变量的话，P值和t值有助于证明模型是否足够吻合线性模型。

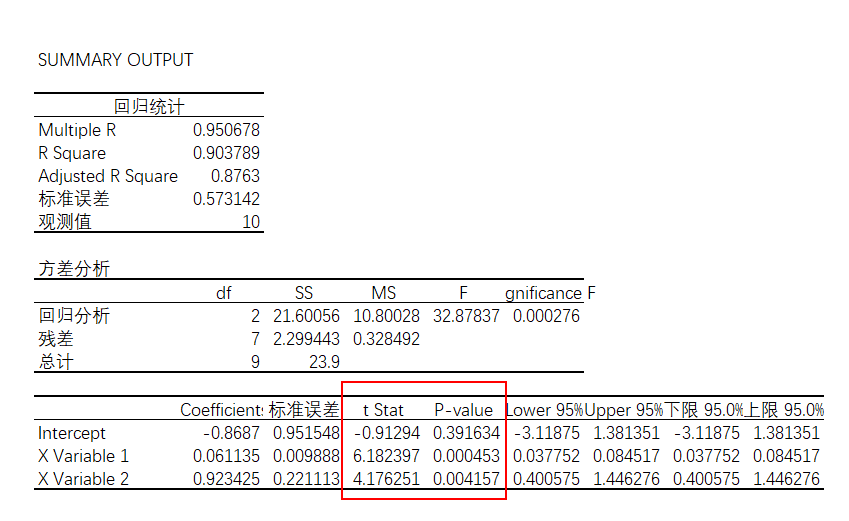
图4-44

T检验是用于小样本（样本容量小于30）的两个平均值差异程度的检验方法。它是用T分布理论来推断差异发生的概率，从而判定两个平均数的差异是否显著。Excel通过这个t值来计算P值，因此可以认为t值是一个中间过程产生的数据，不必理它。

p值（p value）就是当原假设为真时所得到的样本观察结果或更极端结果出现的概率。如果p值很小，说明在原假设下极端观测结果的发生概率很小。而如果出现了，根据小概率原理，我们就有理由拒绝原假设；p值越小，我们拒绝原假设的理由越充分

如果p值是5%，也就是说，如果你以此为界拒绝原假设的话，那么只有5%的可能性犯错。P值越接近于0就代表越不可能犯错。

运输次数的回归系数值为0.923(t=4.176，p=0.004157<0.01)，意味着运输次数会对运输时间产生显著的正向影响关系。运输里程的回归系数值为0.061(t=6.182，p=0.000453<0.01)，意味着运输里程会对运输时间产生显著的正向影响关系。